#color(brown)("y-intercept")# at #x=0# giving: #y=(-3)/(-8)=+3/8#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("x-intercept")# at #y=0# giving:
#0=(x-3)/(-2x-8)#
Multiply both sides by #-2x-8# giving
#0=x-3 -> x=3#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Hole")#
Not 'allowed' to divide by 0 (undefined)
So #-2x-8!=0#
#2x!=-8#
#x!=-8/2 #
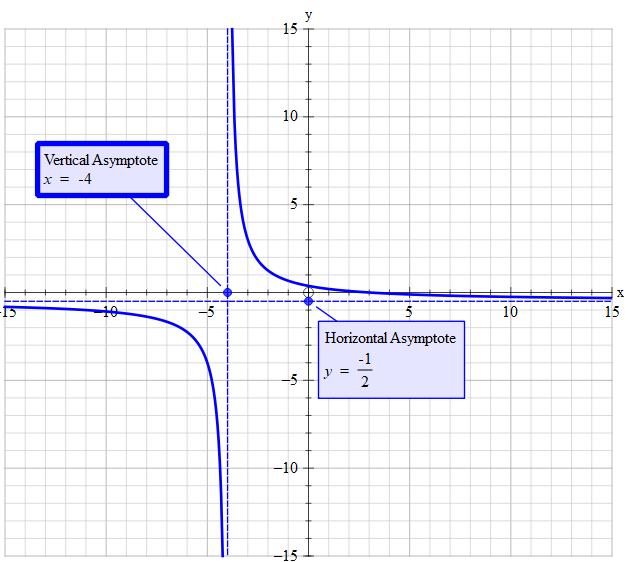
#x!=-4 larr" Hole at "x=4#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Horizontal asymptotes")#
These occur as #x# tends to infinity.
Set #y=(x-3)/(-2x-8)#
As #x# becomes 'larger' in both positive and negative directions the -3 and -8 become insignificant. Consequently the equation is 'tending' towards:
#y=-x/(2x)->-1/2#
#lim_(x->+-oo) (x-3)/(-2x-8)=-1/2#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Vertical asymptotes - positive")#
These will occur as the denominator tend to 0. That is, tends towards any holes. This has to be looked at as you approach it from both the left and right. So lets investigate.
Set #x=-4 + delta# where #0 < delta < 1#
#y=(-4+ delta -3)/((-2(-4+delta)-8)#
#y=(-7+delta)/(-2delta)#
Negative #-:# negative is positive
#7-:"something minute" ->oo#
So from the right
#y=lim_(color(blue)(x->0^(+))) (x-3)/(-2x-8)=+oo#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Vertical asymptotes - negative")#
Using the same approach as above but approaxhing #x=-4# from the left we end up with:
#y=lim_(color(blue)(x->0^(-))) (x-3)/(-2x-8)=-oo#