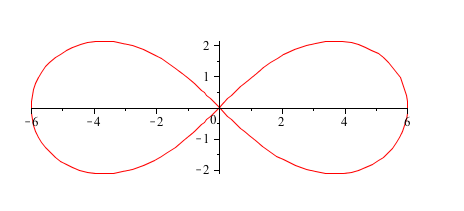
How do you graph the lemniscate #r^2=36cos2theta#?
1 Answer
Hello,
-
You have to graph two curves of polar equations
#r = 6 sqrt(cos(2 theta))# and#r = -6 sqrt(cos(2 theta))# -
It's enough to graph the first one : the second curve is the O-symmetric of the first one. The range is
#{theta in RR | cos(2 theta) >= 0} = bigcup_(k in ZZ) [-pi/4 + k pi , pi/4 + kpi]# -
Reduce the range of
#r# :
1)#r(theta + pi) = r(theta)# : you can study#r# only on#[-pi/4 , pi/4]# .
2)#r(-theta) = r(theta)# : you can study#r# on#[0,pi/4]# but you have to complete the curve with#Ox# -axis. -
Calculate derivative of
#r# :
#r'(theta) = 6 (-2 sin(2 theta))/(2 sqrt(cos(2 theta))) = - 6 sin(2 theta)/sqrt(cos(2 theta))# -
Study the sign of
#r'# on#[0, pi/2]# : because#2theta in [0, pi]# ,#sin(2 theta) >=0# , so#r'(theta) <= 0# and#r# is a decreasing function on#[0, pi/2]# . -
Find particular tangents. Remember that :
1) if#M(theta) \ne O# , the tangent at#M(theta)# is directed by#r'(theta) vec u_(theta) + r(theta) vec v_(theta)# , where#(vec u_(theta) , vec v_(theta))# is the polar basis.
2) if#M(theta)=O# , the tangent at#O# is directed by#vec u_(theta)# .
Here, you have :
1) tangent at
2) tangent at
3) there exists a horizontal tangent :
But,
Finally,
Graph.
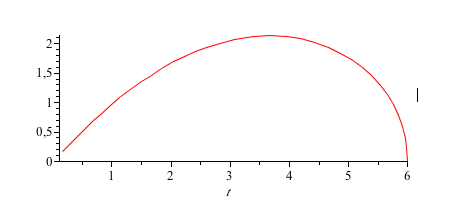
1) On
2) On
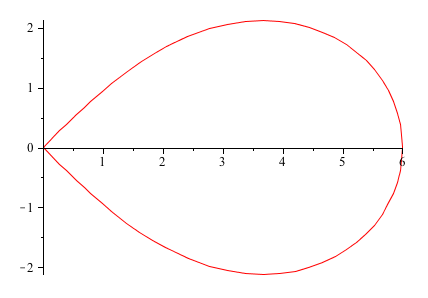
3) Finally the all curve with