Question

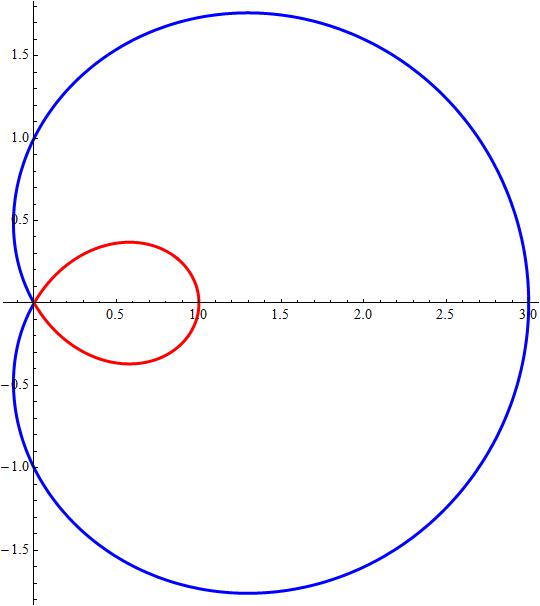
What is the graph of the Cartesian equation `(x^2 + y^2 - 2ax)^2 = b^2(x^2 + y^2)`?

Answer 1

two versions of the same cardioid

`(r+b-2acos(theta))(r-b-2acos(theta))=0`

Explanation:

Taking

`(x^2 + y^2 - 2 a x)^2 - b^2 (x^2 + y^2)=(x^2 + y^2 - 2 a x + b sqrt[x^2 + y^2])(x^2 + y^2 - 2 a x - b sqrt[x^2 + y^2]) = 0`

and then separately, after substituting

#{ (x = r cos(theta)), (y=r sin(theta)) :}#

`x^2 + y^2 - 2 a x + b sqrt[x^2 + y^2] = r+b-2a cos(theta)=0`
`x^2 + y^2 - 2 a x - b sqrt[x^2 + y^2] = r-b-2a cos(theta)=0`

So, in polar coordinates reduces to

`(r+b-2acos(theta))(r-b-2acos(theta))=0` wich are two versions of the same cardioid.

Attached a plot showing in red
`r = -b + 2 a cos(theta), pi/3 < theta < pi/3`
and in blue
`r=b+2acos(theta), -2pi/3 < theta < 2pi/3`

for ·`a = b = 1`