How do you graph #x^2 + (y + 2)^2 = 9#?
1 Answer
Jul 8, 2015
You convert the equation to standard form, determine the centre, vertices, and endpoints. Then you plot the graph.
Explanation:
This is almost the standard form for the equation of a circle.
Let's modify it to read
Now we see that it is a circle with centre at (
This means that, to find the vertices, you go 3 units up from the centre and 3 units down.
Thus, the vertices are at (
To find the endpoints, you go 3 units left of the centre and 3 to the right.
Thus, the endpoints are at (
Plot these points on a graph.
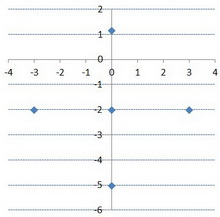
Now draw a smooth circle through these four points.
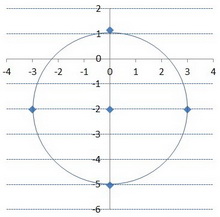
And you have your graph.

