Question

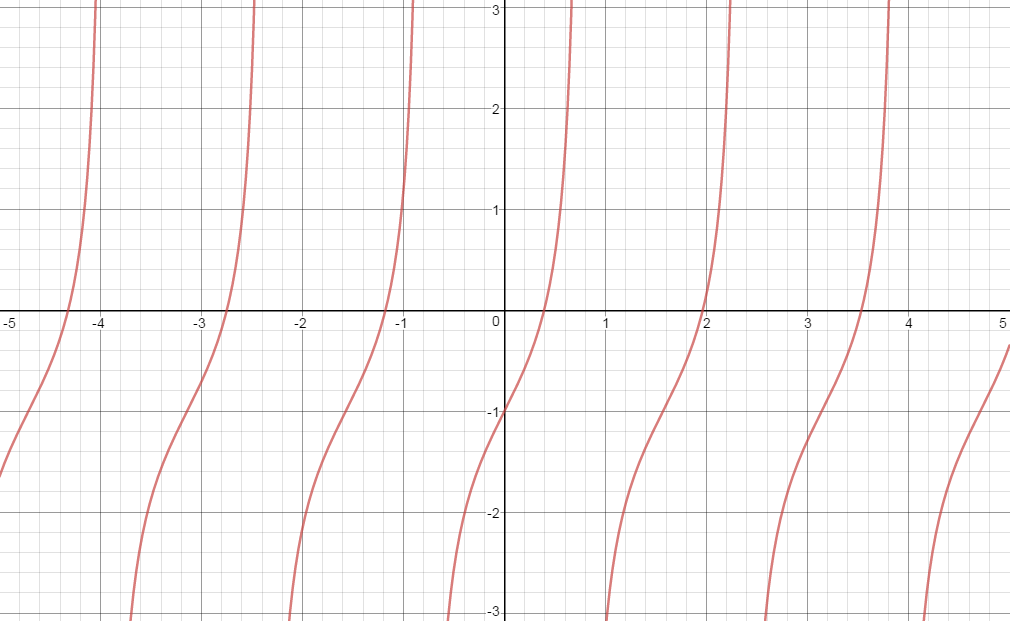
How do you graph `y=-1+tan2x`?

Answer 1

To graph `y=-1+tan 2x`, we determine the x and y intercepts and then add points that will enable to draw graph for 1 period. See the explanation.

Explanation:

The given equation

`y=-1+tan 2x`

Set `x=0` then solve for `y`

`y=-1+tan 2x`

`y=-1+tan 2(0)`

`y=-1`
We have the y-intercept at `(0, -1)`
~~~~~~~~~~~~~~~~~~~~~~~~~

Set now `y=0` then solve for `x`

`y=-1+tan 2x`
`0=-1+tan 2x`

`1=tan 2x`

`arctan (1)=arctan(tan 2x)`

`pi/4=2x`

`x=pi/8`
We have the x-intercept at `(pi/8, 0)`

Other points are `(pi/4, +oo)` and `(-pi/4, -oo)`

Since the graph of `y=-1+tan 2x` is periodic, there will be a repetition of the same graph every `pi/2` period. Kindly see the graph of `y=-1+tan 2x`