How do you graph #y=1/[x(x-2)]#?
1 Answer
You find the intercepts and the asymptotes, and then you sketch the graph.
Explanation:
Step 1. Find the
There is no
Step 2. Find the
There is no
Step 3. Find the vertical asymptotes.
Set the denominator equal to zero and solve for
There are vertical asymptotes at
Step 4. Find the horizontal asymptote.
The degree of the denominator is greater than the degree of the numerator, so
The horizontal asymptote is at
Step 5. Draw your axes and the asymptotes.
The vertical asymptotes divide the graph into three regions of
(a) The left hand region has the
The point at (
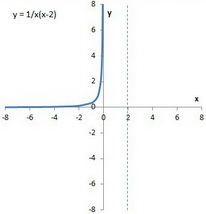
(b) The right hand region has
The point at (
So we have a mirror-image hyperbola in the first quadrant.
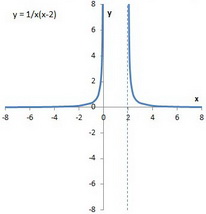
(c) In the middle region, we have
The points at (
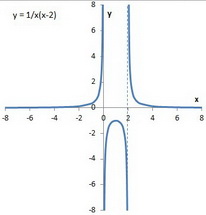
And we have our graph.

