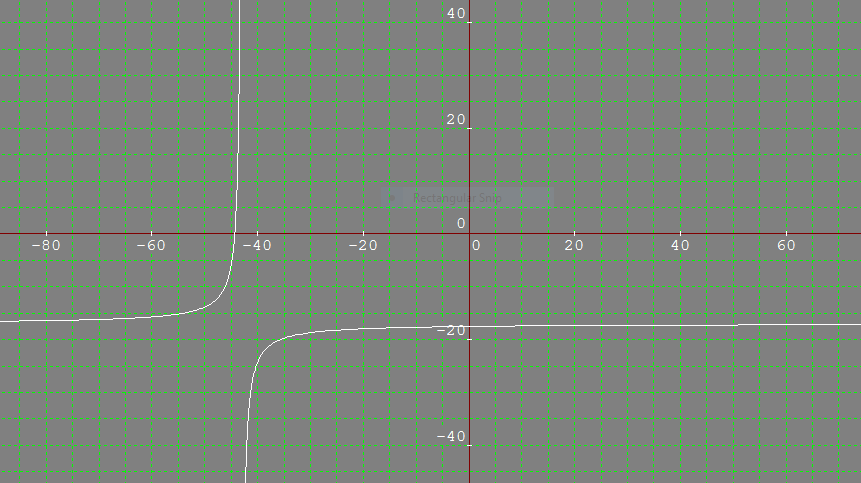
How do you graph #y=-22/(x+43)-17# using asymptotes, intercepts, end behavior?
1 Answer
Nov 4, 2016
Explained below
Explanation:
As
Next, as
The graph will cross y-axis at point (0, -17-22/43) that is (0, -753/43)
The graph would cross x-axis at point y=0 and x coordinate would be given by
The point would thus be ( -753/17,0).The graph would look like