How do you graph #y=(2x+2)/(3x+1)# using asymptotes, intercepts, end behavior?
1 Answer
Sep 22, 2017
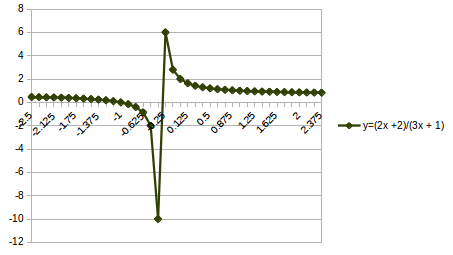
Calculate those critical points, and then the shape and location of the curve will be easier to see.
Explanation:
The intercept (on one side only) is at
The plot is symmetrical around both asymptotes (x = -1/3 and y = 0.666666666)
Ignore the interconnecting line in the plot. It is where the asymptote would go.