Question

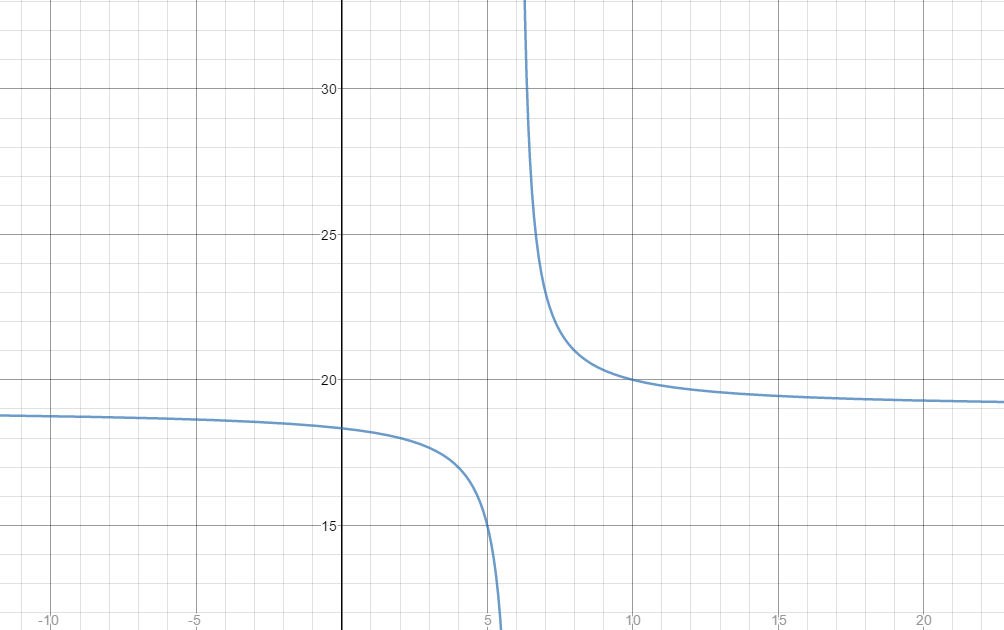
How do you graph `y=4/(x-6)+19` using asymptotes, intercepts, end behavior?

Answer 1

Please read the reference and the explanation.

Explanation:

Multiply both sides by `x - 6`:

`xy - 6y = 4 + 19x - 114`

`xy - 6y = 19x - 110`

This is a rotated Hyperbola.

Here is a helpful Reference

Arrange in accordance with the quadratic equation in the reference:

`xy - 6y - 19x - 110 = 0`

Here are the values of their coefficients:

`A_(xy) = 1/2, B_x = -19/2, B_y = -3, C = -110, and A_("xx") = A_(yy) = 0`

Find the center:

#D = | (A_("xx"), A_(xy)), (A_(xy),A_(yy)) | = | (0,1/2), (1/2,0) | = -1/4#

#x_c = -1/D | (B_x, A_(xy)), (B_y,A_(yy)) | = 4| (-19/2, 1/2), (-3,0) | = 4(3/2) = 6#

#y_c = -1/D | (A_("xx"), B_x), (A_(xy),B_y) | = 4| (0, -19/2), (1/2,-3) | = 4(19/4) = 19#

The center is `(6,19)`

The calculation for the vertices is very long so I will just give them to you `(4,17)` and `(8,21)`

Here is a graph: