Question

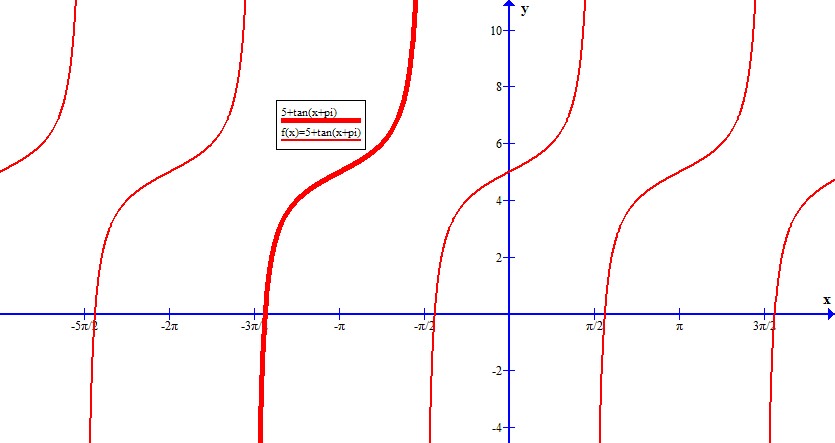
How do you graph `y=5+tan(x+pi)`?

Answer 1

Start from a "basic cycle" for the `tan` function to obtain the results below.

Explanation:

Starting with the "basic cycle" for `tan(theta)` i.e. for `theta in [-pi/2,+pi/2]`

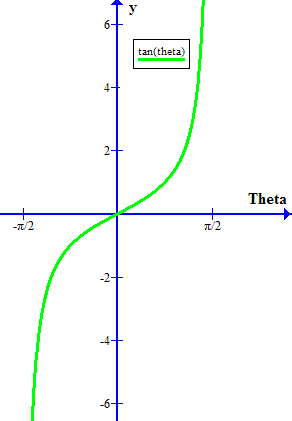
Then consider what values of `x` would place `(x+pi)` in this same range, i.e. `(x+pi) in [-pi/2,+pi/2]`
(Yes; I know: because `tan` has a cycle length of `pi` we could recognize that the cycle will repeat at exactly the same place, but let's do this for the more general case.)
`(x+pi)in[-pi/2,pi/2]color(white)("X"rarrcolor(white)("X")x in [-(3pi)/2,-pi/2]`
Giving us the "basic cycle" for `tan(x+pi)`:

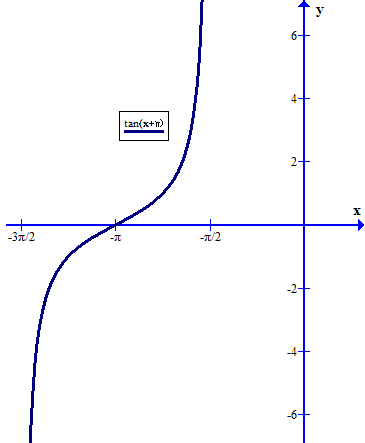
Adding `5` to this to get `y=5+tan(x+pi)` simply shifts the points upward `5` units:

In the image below, I have added the "non-basic cycles" as well as the "basic cycle" used for analysis: