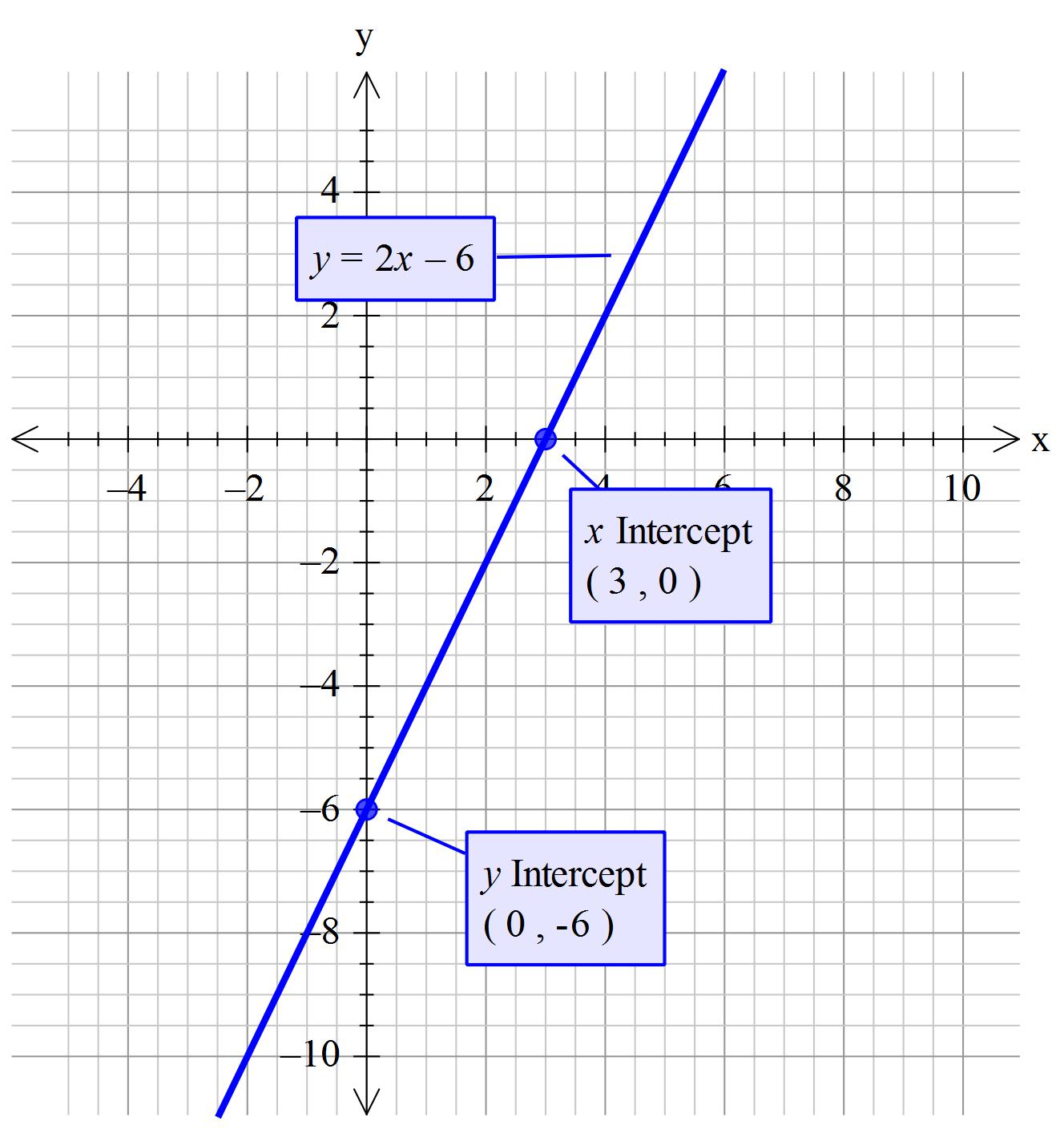
How do you graph #y=-6+2x# using the intercepts?

Question

3583 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-07T16:05:27

#color(blue)(=>y_("intercept") ->(x,y) = (0,-6))#

#color(blue)(=>x_("intercept") ->(x,y) = (3,0))#

Find the points of intercepts and draw a line through them.

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the "x" intercept")#

The line crosses the x-axis at #y=0# so by substitution we have:

#color(brown)(y=2x-6)color(green)(" "->" "0=2x-6)#

Add 6 to both side so that the 6 on the right becomes 0

#6=2x+0#

Divide both sides by 2 so that the 2 from #2x# becomes 1. This is because #1xx x=x#. That is, you get rid of the 2 on the right.

#6/2=2/2xx x#

#3=x#

#color(blue)(=>x_("intercept") ->(x,y) = (3,0))#

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the "y" intercept")#

The line crosses the y-axis at #x=0# so by substitution we have:

#color(brown)(y=2x-6)color(green)(" "->" "y=2(0)-6)#

But #2xx0=0#

#y=0-6#

#y=-6#

#color(blue)(=>y_("intercept") ->(x,y) = (0,-6))#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Tony B