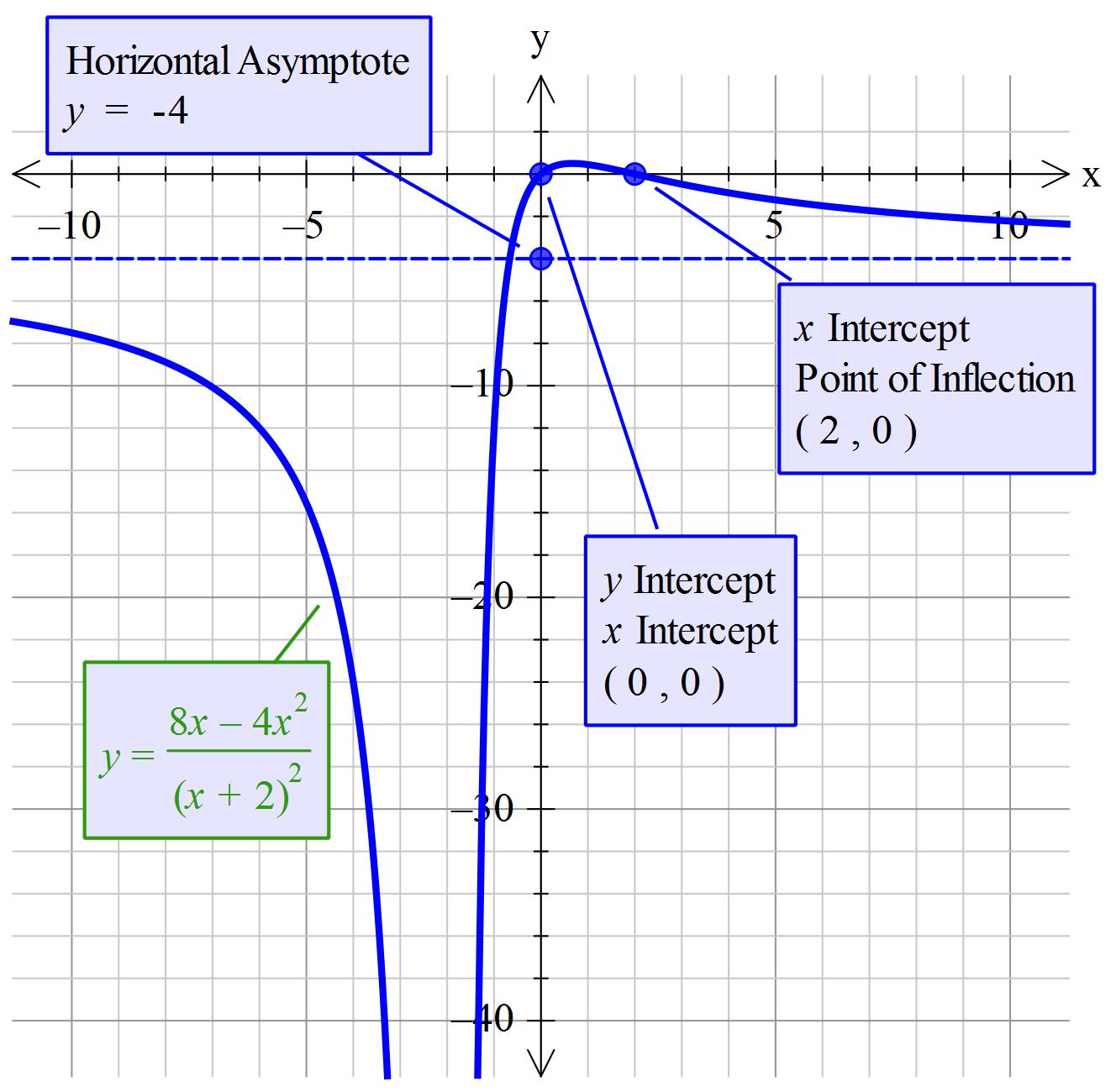
#color(blue)("Investigating extremities")#
#color(brown)(y=Lim_(x->+-oo) (8x-4x^2)/((x+2)^2)->color(blue)((-4(+-x)^2)/((+-x)^2) = -4)#
Note that #x^2" " underline("'wins'")# over the other values in this equations
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Investigating "x=0)#
#color(brown)(y= (8x-4x^2)/((x+2)^2)->color(blue)(0/4=0)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Investigating "y=0)#
#=>8x=4x^2#
#color(blue)(=> x=2)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)(x_("intercepts") -> (x,y)-> (0,0)" and "(2,0)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)(y_("intercepts")->(x,y)-> (0,0) )#
"'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("The equation is undefined at "x=-2" (excluded value)")#
Let #deltax# be very small
Let #x-2#
Then we have
#y=(8(-2+deltax) -4(-2+deltax)^2)/([(-2+deltax)+2]^2)#
#y=(-16+8deltax-4(4-4deltax+(deltax)^2))/((deltax)^2)#
#y=(-16+8deltax-16+16deltax-4(deltax)^2)/((deltax)^2)#
#y=-32/((deltax)^2) +24/(deltax)-4#
as #deltax# becomes increasingly small then #|-32/((deltax)^2)| >24/deltax# .
#color(brown)(y=lim_(deltax->0) -32/((deltax)^2) +24/(deltax)-4)color(blue)(-> -oo)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~