Question

How do you graph `y=cos(2x)` over the interval `0<=x<=360`?

Answer 1

Remember the `cos` function has the following points:
`(0,1),(90,0),(180,-1),(270,0),(360,1)`

Explanation:

But because it `2x` the period is shortened. It will reach its `0-`point after only 45, the `-1` after 90, etc.

So the points are now:
`(0,1),(45,0),(90,-1),(135,0),(180,1),(225,0),(270,-1),(315,0),(360,1)`
(vertical axis on the graph below should be read as 100=1)
graph{100cos(2pix/180) [-27.8, 453, -127.5, 113.2]}

Answer 2

Graph would look like as shown below.

Explanation:

Select a trignometric graph and plot the following points and join with a smooth curve, as shown. This completes two cycles of this periodic function.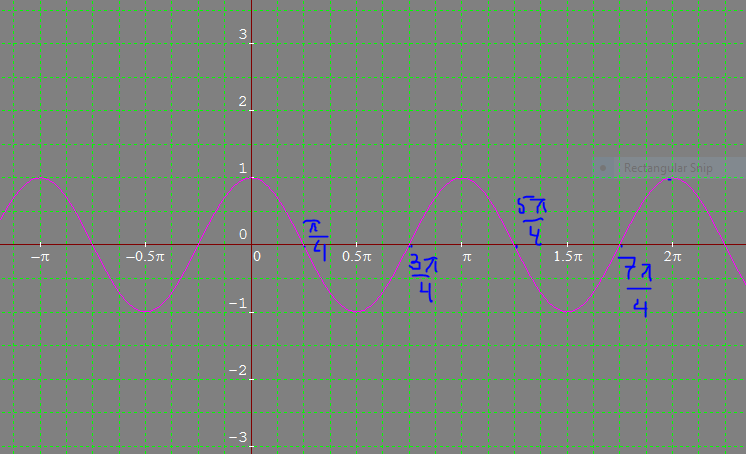

`(0,1) ; (pi/4,0); (pi/2, -1); ((3pi)/4,0) :( pi, 1); ((5pi)/4,0); ((3pi)/2, -1); ((7pi)/4, 0) and (2pi, 1).`

Join the points with a smooth curve as shown in the graph.

                              *********