How do you graph #y=-cos2x#?
1 Answer
See the explanation, please. By observing graphs we can understand how transformation takes place.
Explanation:
Given:
We need to graph this function.
To understand the behavior of this graph, we can draw the following graphs and then compare them:
First, we will start graphing
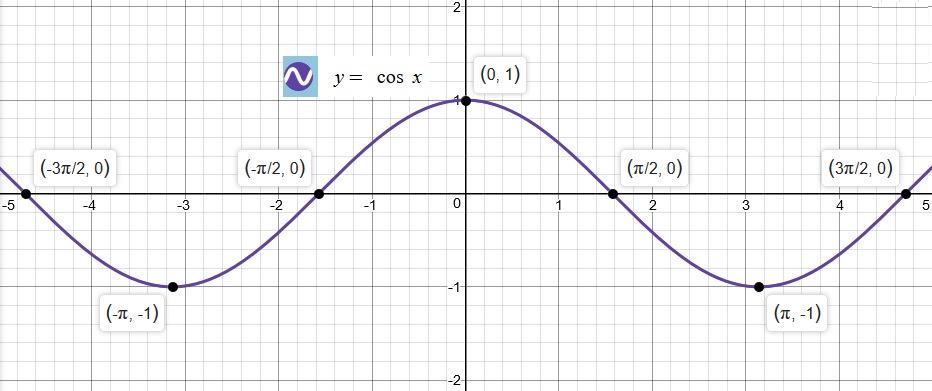
Then we will graph
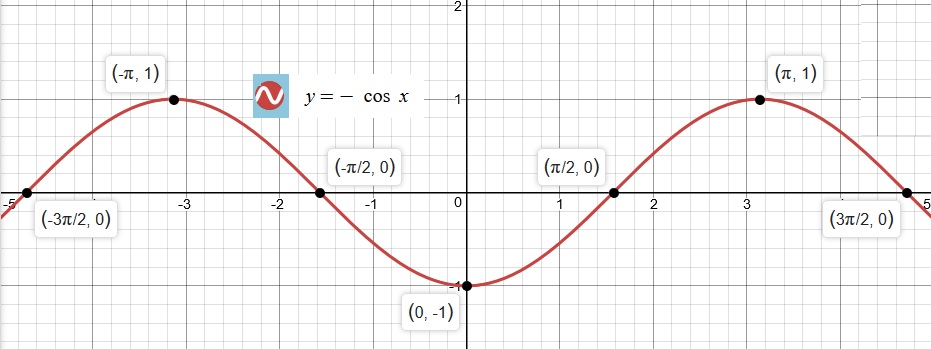
Then we will graph
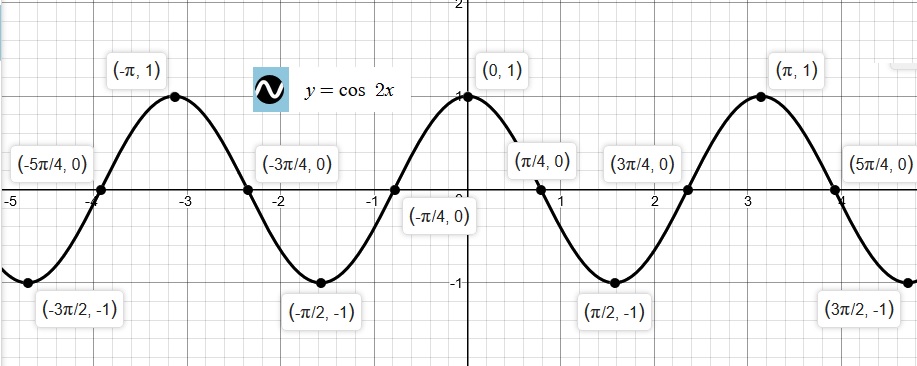
Then we will graph
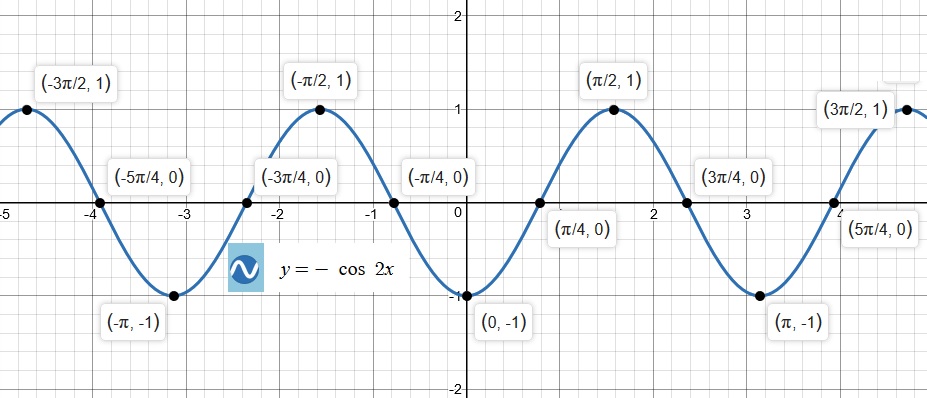
Next, we will observe all of the above graphs as one:
KEY for the graphs:

Now the graphs ...
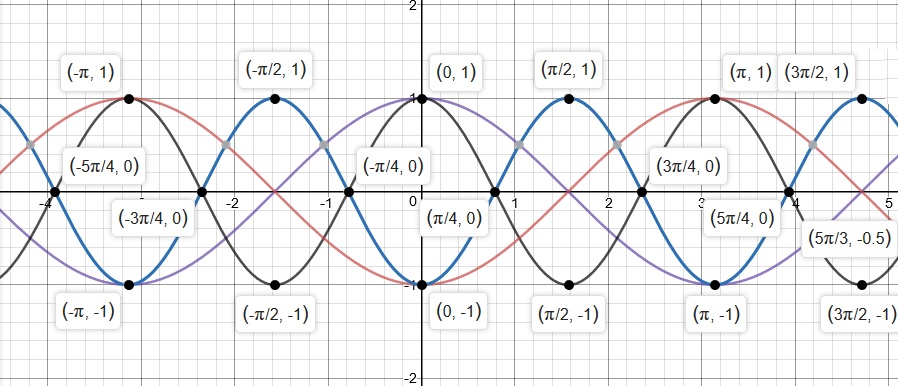
We observe the following in the graph of
The domain of
The function has no undefined points nor domain constraints.
Therefore domain is
As the
To be precise, the function
The function
The function
Amplitude of the function
If a point

