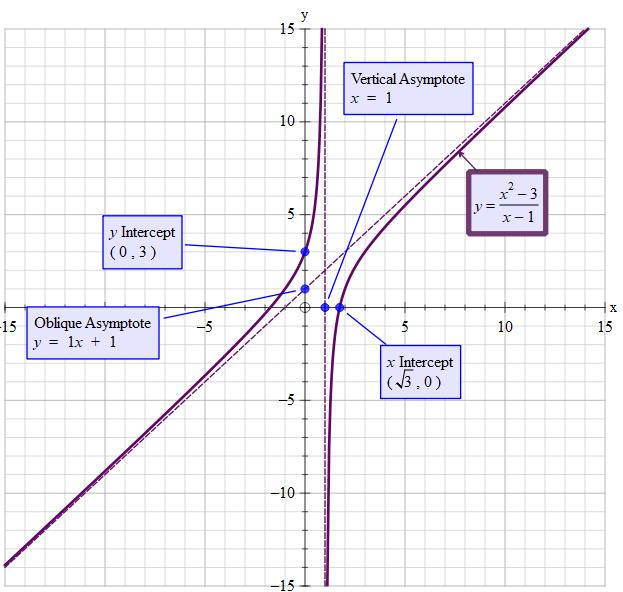
How do you graph #y =(x^2-3)/(x-1)#?
1 Answer
See explanation
Explanation:
If you are dealing with questions at this level you know how to find the
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Undefined at
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If we have
Then we have
x -> 0^+
Conversely
If we have
Then we have
x-> 0^-
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The temptation is to state the the const values become insignificant so we end up with
THIS IS WRONG
If we actually divide the denominator into the numerator we get
Now when we take limits we end up with
Set