How do you graph y=x^2-9?
2 Answers
Please read the explanation.
Explanation:
A quadratic equation is of the form:
We have :
Set
We have the quadratic equation:
Using the algebraic identity:
We can rewrite
Hence, there are two solutions for
So, we have two x-intercepts:
To find the y-intercept, set
Hence, the y-intercept:
The graph of
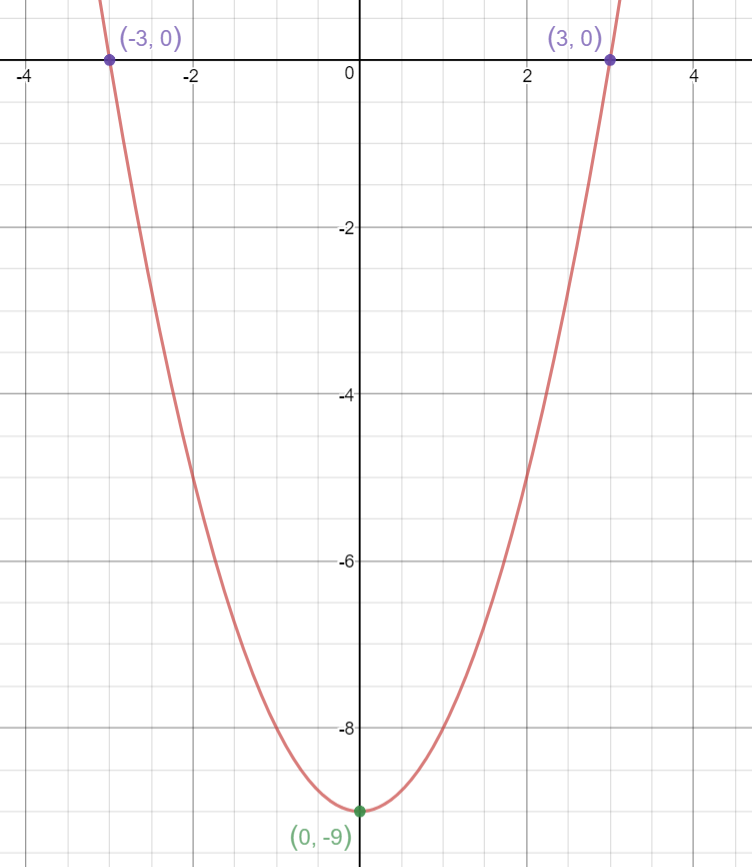
Hope it helps.
Refer to the explanation.
Explanation:
Given:
where:
To graph a quadratic equation in standard form, you need the vertex, y-intercept, x-intercepts (if real), and one or two additional points.
Vertex: maximum or minimum point
Since
The x-coordinate of the vertex is determined using the formula for the axis of symmetry:
To find the y-coordinate of the vertex, substitute
The vertex is
In this case, the vertex is also the y-intercept, which is the value of
X-intercepts: values for
Substitute
Switch sides.
Factor
Set each binomial equal to
Point:
Point:
For additional points, choose values for
Plot all the points and sketch a parabola through the points. Do not connect the dots.
graph{y=x^2-9 [-11.13, 11.37, -9.885, 1.365]}


