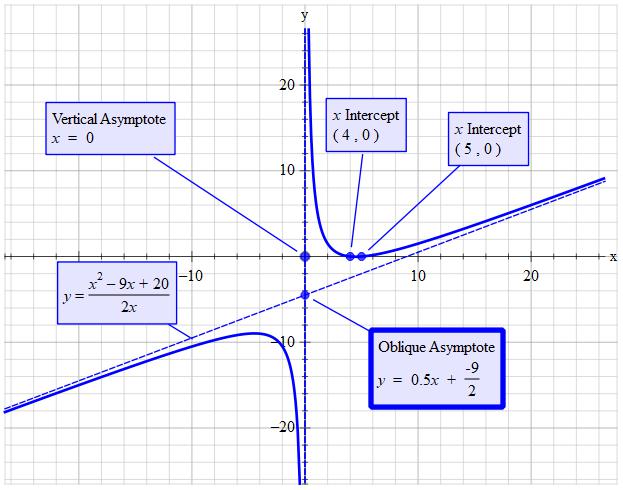
Given: #y=(x^2-9x+20)/(2x)#
First and foremost, the equation becomes undefined when the denominator is 0
Thus #2x!=0 => x!=0 larr "Asymptote"#
The true behaviour can be determined if we carry out the division.
#y=x/2-9/2+10/x#
#color(blue)("Consider the case "lim_(x->0^("+"))#
#y=lim_(x->0^("+")) x/2-9/2+lim_(x->0^("+"))(10/x)#
#y=0-9/2+oo = oo#
#color(blue)("Consider the case "lim_(x->0^("-"))#
#y=lim_(x->0^("-")) x/2-9/2+lim_(x->0^("-"))(10/x)#
#y=0-9/2-oo = -oo#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Consider the case " lim_(x->+oo) )#
#y = lim_(x->+oo)x/2-9/2+lim_(x->+oo)10/x#
#y=oo-9/2+0 = oo#
#color(brown)("Observe the this is of general form ")#
#color(brown)(y=1/2x-9/2 larr" Asymptote")#
#color(blue)("Consider the case " lim_(x->-oo) )#
#y = lim_(x->-oo)x/2-9/2+lim_(x->-oo)10/x#
#y=-oo-9/2+0 = -oo#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Are there any "x" intercepts?")#
Set #y=0=1/2x +10/x-9/2#
#0=(x^2-9x+20 )/(2x)#
#0=x^2-9x+20#
#0=(x-9/2)^2+20-81/4#
#(x-9/2)^2=1/4#
#x=9/2+-1/2#
#x=4 and 5#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~