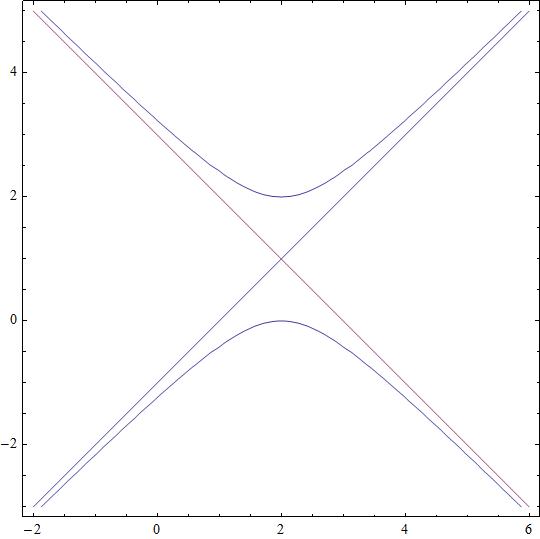
#f(x,y) = y² - x² - 2y + 4x - 4 =0# is a conic
The kind of conic can be answered after analyzing its associated quadratic form.
#q_f(x,y) =1/2 {x,y}((f_{x x},f_{x y}),(f_{y x},f_{y y})){x,y}#
where #f_{x_1,x_2} =( partial^2f)/(partial x_1 partial x_2)#
Here
#((f_{x x},f_{x y}),(f_{y x},f_{y y}))=((-2,0),(0,2))# with eigenvalues #{-2,2}# which characterize this conic as a Hyperbole.
The hyperbole canonic representation is
#h(x,y)=1/2{x-x_0,y-y_0}((-2,0),(0,2)){x-x_0,y-y_0}+c_0#
Now, comparing
#f(x,y)=h(x,y)# we obtain the conditions:
#{
(x_0^2 - y_0^2-4-c_0 = 0), (2 y_0-2 = 0), (4 - 2 x_0 =0)
:}#
Solving for #x_0,y_0,c_0# gives
#{x_0 = 2, y_0 = 1, c_0 = -1}#
so the hyperbole is
#h(x,y)=1/2{x-2,y-1}((-2,0),(0,2)){x-2,y-1}-1#
centered at #{2,1}#
#(y-1)^2-(x-2)^2-1=0->(y-x+1)(y+x-3)-1=0#
so the assymptotes are
#y-x+1=0# and #y+x-3=0#