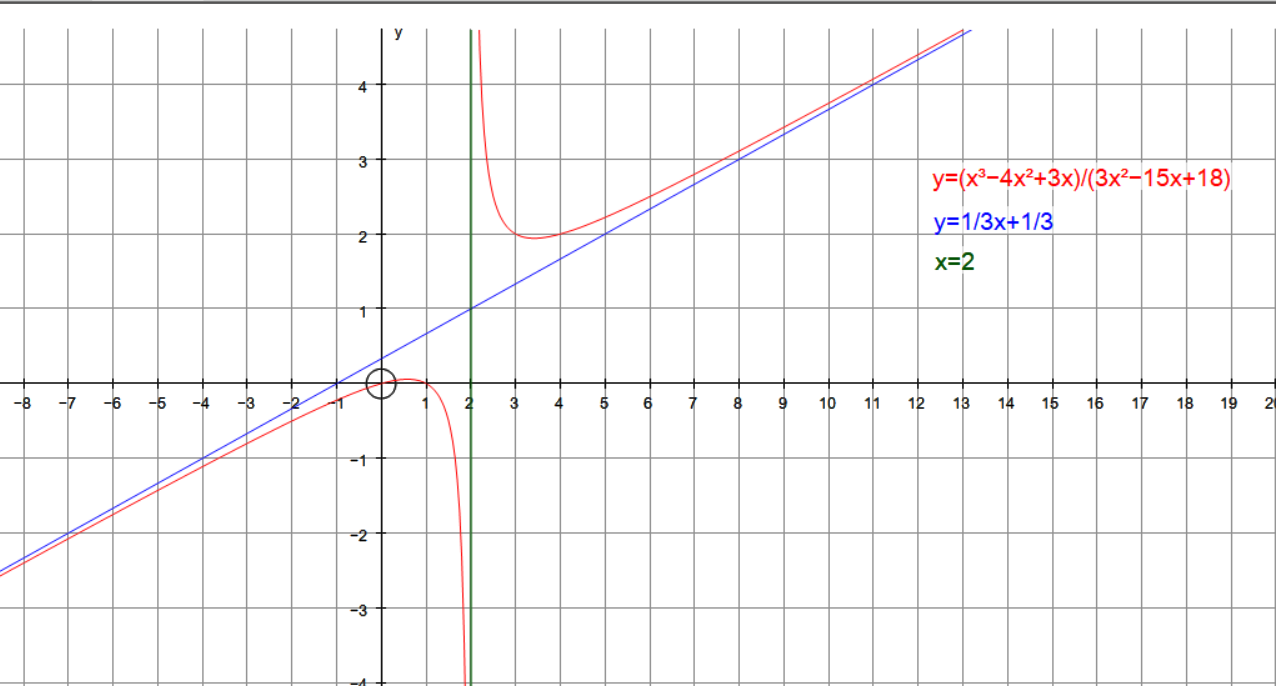
How do you identify all asymptotes or holes for #f(x)=(x^3-4x^2+3x)/(3x^2-15x+18)#?
1 Answer
See below.
Explanation:
First try to factor numerator and denominator:
Notice we can cancel the factor
So there is a hole at
Vertical asymptotes occur where the function is undefined. This occurs when
So the line
The degree of the numerator is greater than the degree of the denominator, so there will be an oblique asymptote. Will can find the equation of this by polynomial division.
We only need to divide until we have the equation of a line, so the remainder of 2 in this case is irrelevant to us.
So the line
For end behaviour, we only need concentrate on:
as
as
GRAPH: