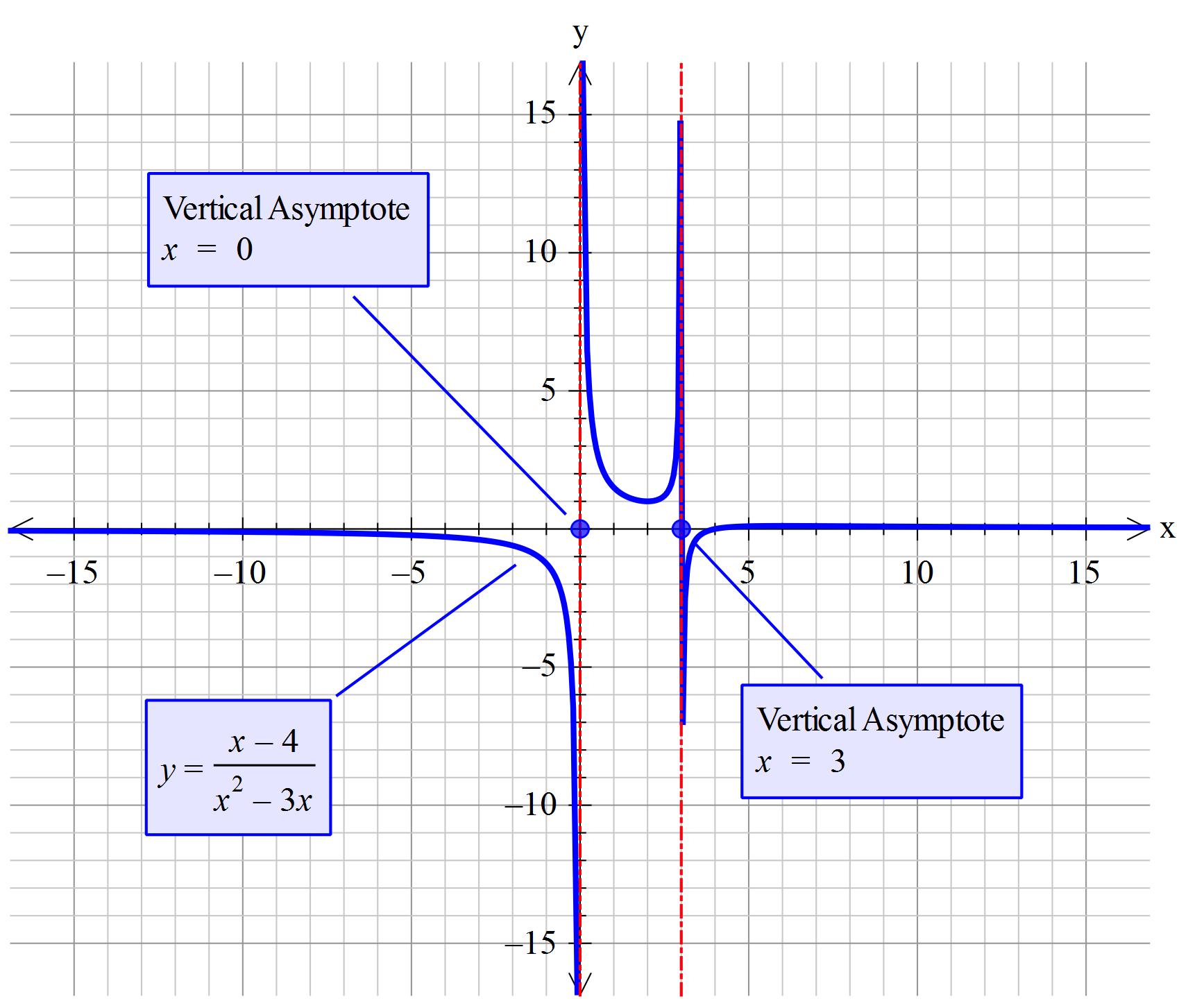
To determine asymptotes you have understand the behaviour of the equation. Some equations are more challenging than others.
#color(blue)("Denominator approaching 0")#
It is 'bad news' to have a denominator become zero.
None technical term for this is 'not allowed'. Correct name is: undefined.
So solve for #x^2-3x=0#
#x(x-3)=0 => x=0" and "x=3#
Consider the case #x=0#
#color(brown)("Suppose "x" tended to 0 from the right (positive)")#
Then writing the equation as:
#f(x)=(x-4)/(x(x-3)) -> (x/x-4/x)/(x-3)#
Then this is almost but not quite the same as:
#lim_(xto0) f(x)=L -> (1-oo)/-3 ->+oo#
#color(brown)("Suppose "x" tended to 0 from the left (negative value"->-x")")#
#f(x)=(x-4)/(x(x-3)) -> ((-x)/(-x)-4/(-x))/((-x)-3)#
Then this is almost but not quite the same as:
#lim_(xto0) f(x)=L -> (1+oo)/-3 ->-oo#
#color(green)("You have the same situation for "x" tending to 3")#
#color(green)("See if you can work that one out using the same method as above")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)(x" tending to "+-oo)#
#f(x)=(x-4)/(x(x-3)) -> (x/x-4/x)/(x-3)#
As #x# becomes larger and larger the 3 in #x-3# has less and less effect. In the end it becomes so insignificant you can forget about it
In the same way #4/x# becomes smaller and smaller the larger #x# becomes. In the end it tends to 0
So #lim_(x->+oo) f(x) -> 1/oo ->0#
So #lim_(x->-oo) f(x) -> 1/(-oo) ->0#