Question

How do you identify the vertical asymptotes of `f(x) = (x+6)/(x^2-9x+18)`?

Answer 1

I found:
`x=6`
`x=3`

Explanation:

You identify the vertical asymptotes by setting the denominator equal to zero: this allows you to see which `x` values the function cannot accept (they would make the denominator equal to zero).
So, set the denominator equal to zero:
`x^2-9x+18=0` solve using the Quadratic Formula:
`x_(1,2)=(9+-sqrt(81-72))/2=(9+-3)2` so you get:
`x_1=6`
`x_2=3`
So your function cannot accept these values for `x`;
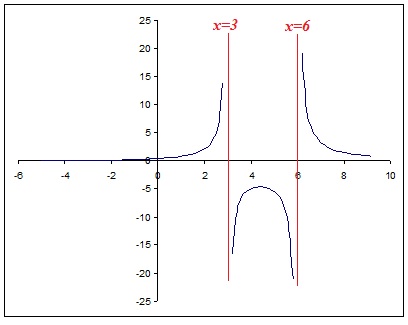
The two vertical lines of equations:
`x=6`
`x=3`
will be your "forbidden" lines or vertical asymptotes.

Graphically: