How do you identity if the equation #2x^2+3x-4y+2=0# is a parabola, circle, ellipse, or hyperbola and how do you graph it?
1 Answer
Feb 23, 2017
The given equation is a Parabola.
Explanation:
Given -
#2x^2+3x-4y+2=0#
The general for of the conic equation can be written as
#Ax^2+Cy^2+Dx+Ey+F=0#
In such case -
If
In the given equation
The coefficeint of
In the given equation
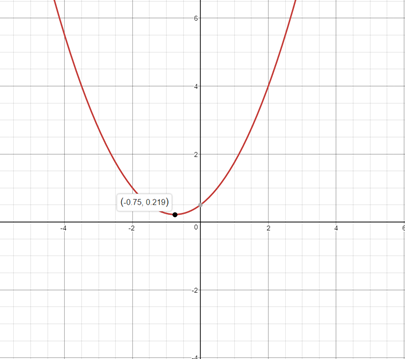
To graph the equation, solve it for
#4y=2x^2+3x+2 #
#y=0.5x^2+0.75x+0.5#
Find its vertex
#x=(-b)/(2a)=(-0.75)/(2 xx 0.5)=-0.75#
Take a few points on either side of
Calculate the corresponding
Tabulate them

Plot the point on a graph sheet. connect them with a smooth curve.