Question

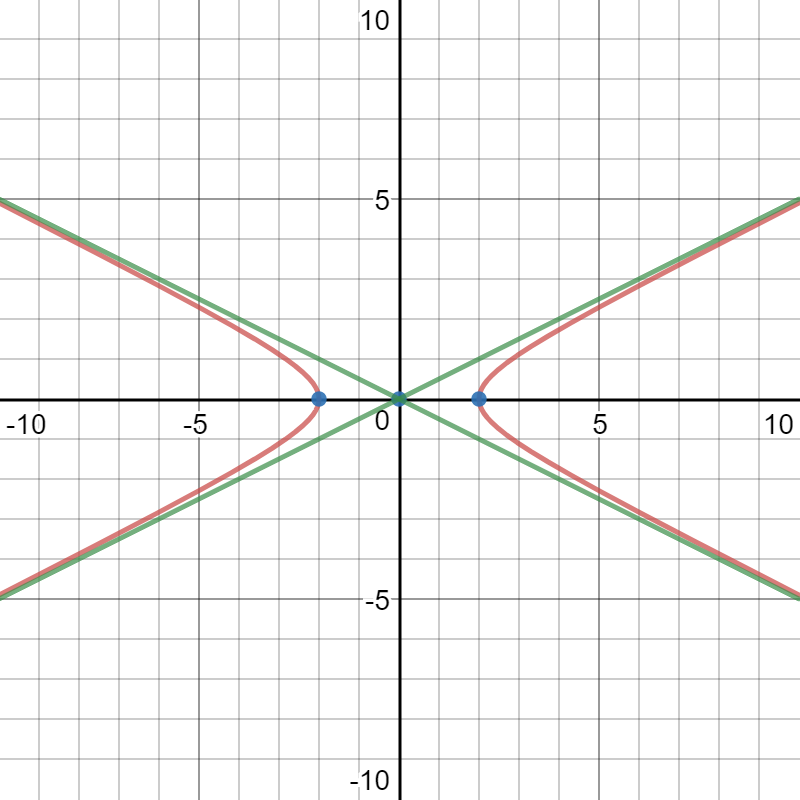
How do you identity if the equation `4y^2-x^2+4=0` is a parabola, circle, ellipse, or hyperbola and how do you graph it?

Answer 1

I wold say an hyperbola:

Explanation:

Have a look:

Answer 2

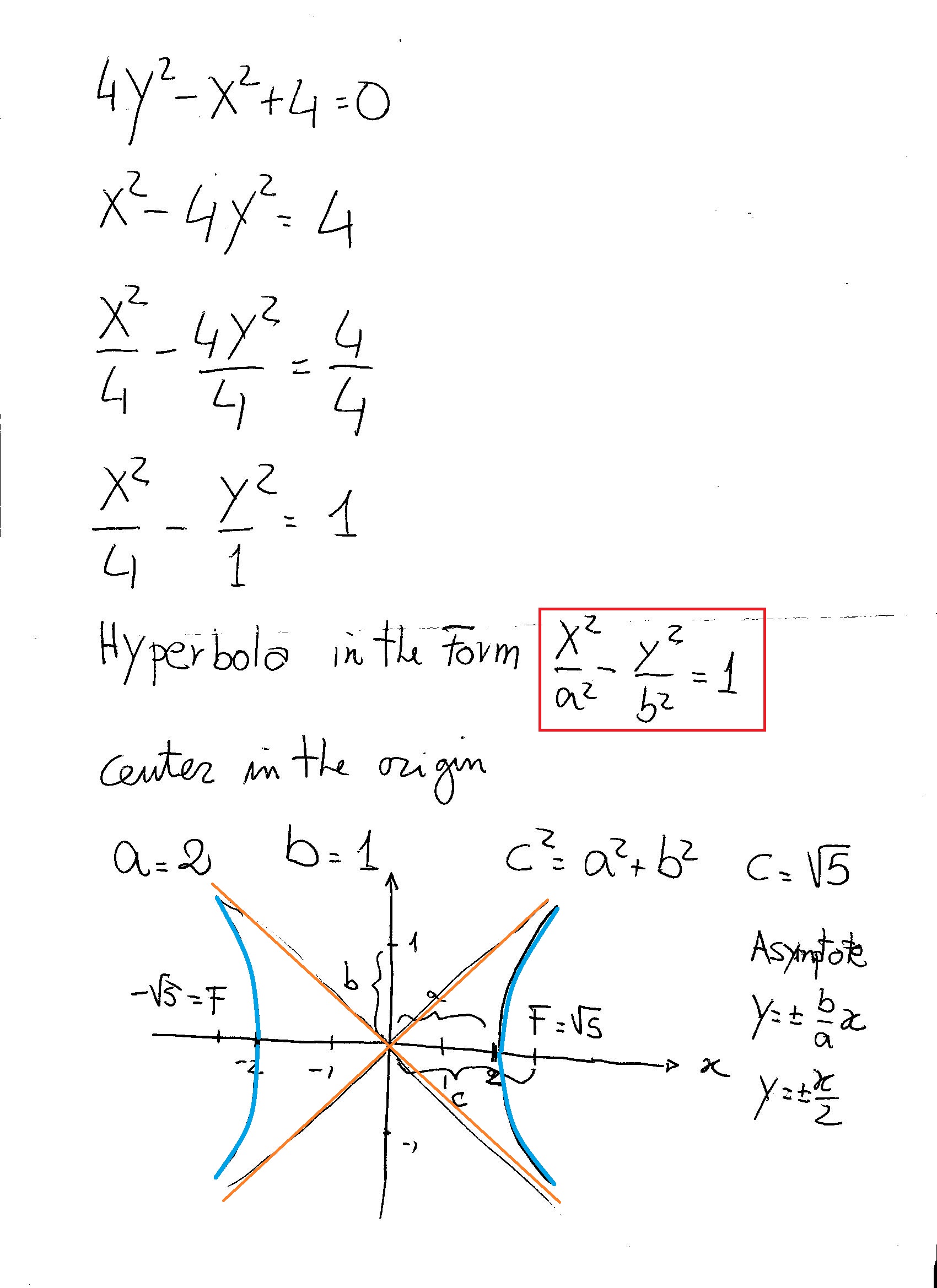
Please seen the explanation.

Explanation:

When given an equation in the form that you have been given, you can use the general Cartesian form for a conic section:

`Ax^2+ Bxy+Cy^2+Dx+Ey+F = 0" [1]"`

Please observe that slight rearrangement of the given equation,

`-x^2+ 4y^2+4=0" [2]"`

Fits equation [1] with:

`A = -1, B = 0, C = 4, D = 0, E = 0 and F = 4`

The section of the reference, entitled Discriminant, tells you how to determine what it is:

`B^2-4(A)(C) = 0^2-4(-1)(4)`

`B^2-4(A)(C) = 16`

`16 > 0`

The fact that the discriminant is greater than 0 tells us that the equation describes a hyperbola.

Subtract for 4 from both sides of equation [2]:

`-x^2+ 4y^2= -4`

Divide both sides by -4:

`x^2/4- y^2 = 1" [3]"`

This fits the standard form `(x-h)^2/a^2-(y-k)^2/b^2= 1" [4]"`

I will fill in the equation to help you see it:

`(x-0)^2/2^2- (y-0)^2/1^2 = 1" [5]"`

Please observe that equation [5] matches the variables of equation [4]:

`h = 0, k = 0, a = 2 and b = 1`

The form for equation [4] is important for graphing because of the following reasons:

1. Everything is centered about the point `(h,k) = (0,0)`
2. The vertices of the hyperbola are located at `(h-a,k) = (-2,0) and (h+a,k) = (2,0)`
3. The equations of the asymptotes are `y = -b/a(x-h)+k and y = -b/a(x-h)+k` which are the two lines `y = -1/2x and y = 1/2x`

This should help you to graph it.

Here is a graph of the hyperbola (red) with the vertices and the center (blue) and the asymptotes (green).