How do you identity if the equation #7x^2-28x+4y^2+8y=-4# is a parabola, circle, ellipse, or hyperbola and how do you graph it?
1 Answer
Please open this link General Cartesian Form in another tab and read, carefully.
Explanation:
From the reference, the General Cartesian Form is:
Rewriting the given equation in the form:
We observe that
Compute the discriminant:
According to the conditions described in the reference, the discriminant is less than zero, therefore, the equation describes an ellipse.
Because
Because
Factor a 7 out of the first 3 term and a 4 out of the next 3 terms:
Use the expansions of
and
to match the middle terms with the middle terms in equation [4]:
To find the value of h, use the equation:
To find the value of k, use the equation:
Substitute
Substitute -1 for k and 2 for h:
Divide both sides of the equation by 28:
Write the denominators as squares:
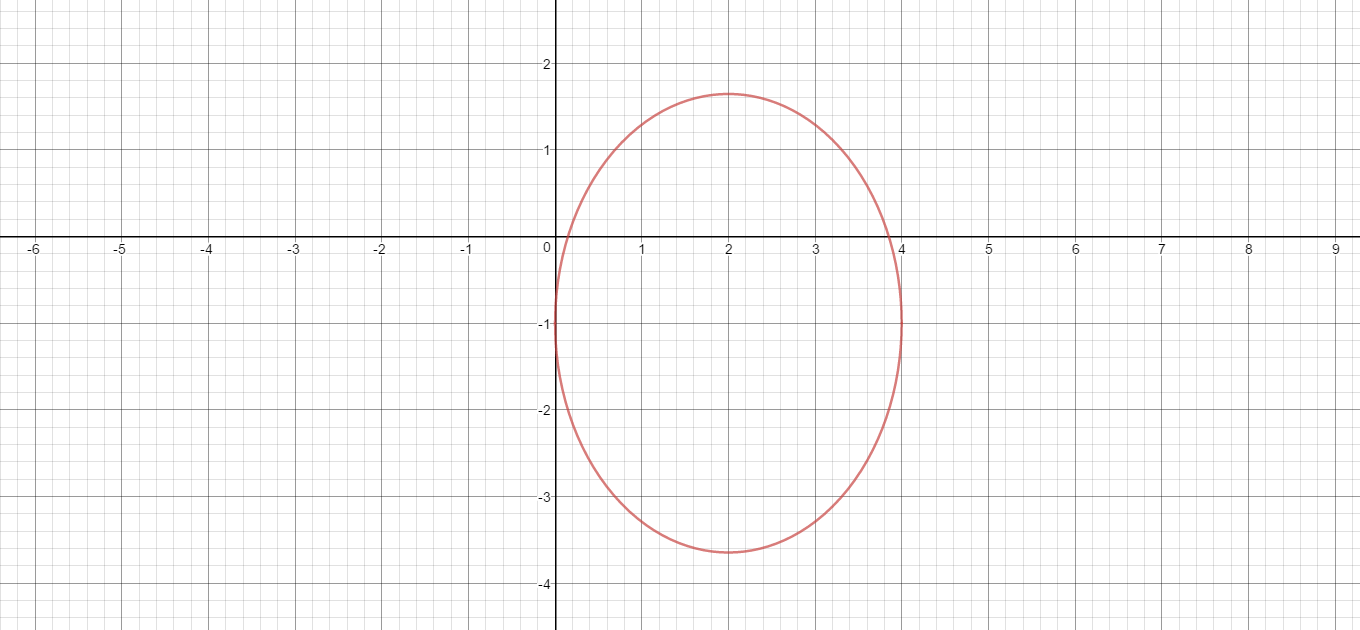
The center is
The major axis end points are
The minor axis end points are
Here is a graph: