Question

How do you identity if the equation `(x-1)^2-9(y-4)^2=36` is a parabola, circle, ellipse, or hyperbola and how do you graph it?

Answer 1

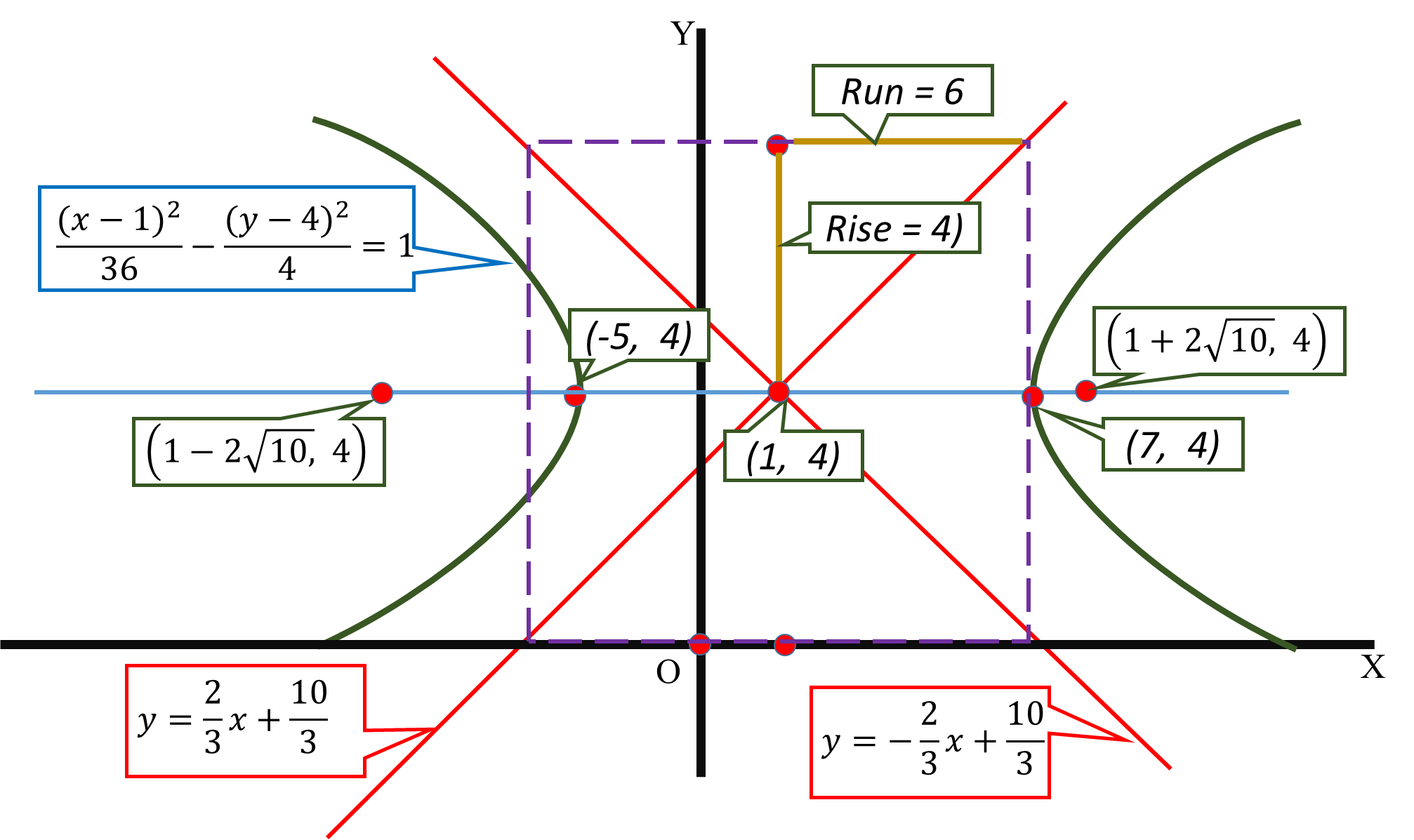
It is a hyperbola.
Its center is `(1, 4)`
Its vertices are :`(7, 4) ; (-5, 4)`
Its foci `(1+-2sqrt10, 4)`
Asymptots; `y=+-2/3x+10/3`

Explanation:

Given -

`(x-1)2-9(y-4)^2=36`

It is a hyperbola.

We shall write it in the standard form -

`(x-1)/36-(9(y-4)^2)/36=36/36`
`(x-1)/36-(y-4)/4=1`

It is in the form

`(x-h)^2/a^2-(y-k)^2/b^2=1`

Its center is `(1, 4)`

Since the `(x-1)/36`term is positive it opens right and left

Its vertices are :

`(x+a, y)`
`a^2=36`
`a=6`
`(1+6, 4)`
`(7, 4)`
`(x-a, y)`
`(1-6, 4)`
`(-5, 4)`

Its foci are -

`f=sqrt(a^2+b^2)`
`f=sqrt(36+4)=sqrt40`
`f=sqrt40=2sqrt10`

`(1+-2sqrt10, 4)`

Asymptots

`y-y_1=m(x-x_1)`

`m=`Rise/run`(Deltay)/(Deltax)=4/6=2/3`

`y-4=2/3(x-1)`

`y=2/3x-2/3+4`

`y=+-2/3x+10/3`