How do you integrate #int (25-x^2)/sqrt(x^2+4)dx# using trigonometric substitution?
2 Answers
Explanation:
We will want to use the substitution
#I=int(25-x^2)/sqrt(x^2+4)dx=int(25-4tan^2theta)/sqrt(4tan^2theta+4)(2sec^2thetacolor(white).d theta)#
Note that
#I=int(25-4tan^2theta)/(2sectheta)(2sec^2theta)d theta=int(25-4tan^2theta)(sec theta)d theta#
Expanding and writing
#I=25intsecthetacolor(white).d theta-4intsin^2theta/cos^3thetad theta#
Rewrite
#I=25intsecthetacolor(white).d theta-4int(1-cos^2theta)/cos^3thetad theta#
#I=25intsecthetacolor(white).d theta-4int(sec^3theta-sectheta)d theta#
#I=29intsecthetacolor(white).d theta-4intsec^3thetacolor(white).d theta" "" "color(red)((star))#
We will tackle
#{(u=sectheta,=>,du=secthetatanthetacolor(white).d theta),(dv=sec^2thetacolor(white).d theta,=>,v=tantheta):}#
Then, using
#I=29intsecthetacolor(white).d theta-4(secthetatantheta-intsecthetatan^2thetacolor(white).d theta)#
#I=29intsecthetacolor(white).d theta-4secthetatantheta+4intsecthetatan^2thetacolor(white).d theta#
Now letting
#I=29intsecthetacolor(white).d theta-4secthetatantheta+4intsectheta(sec^2theta-1)d theta#
#I=25intsecthetacolor(white).d theta-4secthetatantheta+[4intsec^3thetacolor(white).d theta]#
Returning to
#I=25intsecthetacolor(white).d theta-4secthetatantheta+[29intsecthetacolor(white).d theta-I]#
Combining and adding
#2I=54intsecthetacolor(white).d theta-4secthetatantheta#
#I=27intsecthetacolor(white).d theta-2secthetatantheta#
The antiderivative of
#I=27lnabs(tantheta+sectheta)-2secthetatantheta#
Our original substitution was
From this we can say that
#I=27lnabs(x/2+1/2sqrt(x^2+4))-2(1/2sqrt(x^2+4))x/2+C#
Factoring
#I=27lnabs(x+sqrt(x^2+4))-1/2xsqrt(x^2+4)+C#
Explanation:
Recognize trig substitution in denominator from radical, so list various useful trigonometric ratios with this triangle.
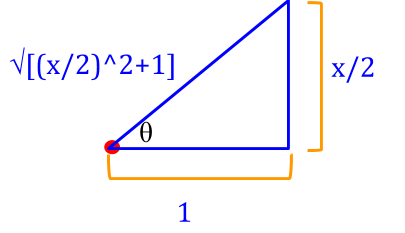
Now, we're getting close to the end - we have to simplify
Use integration by parts:
Lastly, re-substitute the trig ratios:
Change the square root notation back to the original form:


