We have:
#int_-3^-2 1/(sqrt(x^2-1))dx#
We use the fundamental theorem of calculus:
#int_a^bf(x)dx=F(b)-F(a)# when #F'(x)=f(x)#
What is #int1/(sqrt(x^2-1))dx#?
We use the trigonometric substitution.
Since the variable is getting subtracted by one, this is the secant case.
We draw a right triangle:
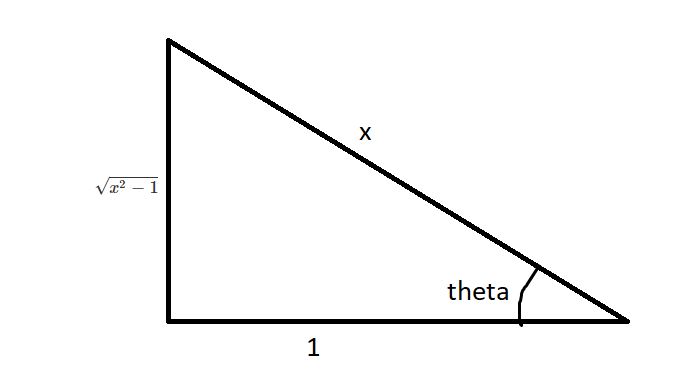
We see that:
#sec(theta)=x#
#=>theta=arcsec(x)#
#=>sec(theta)tan(theta)d theta=dx#
#tan(theta)=sqrt(x^2-1)/1#
#=>tan(theta)=sqrt(x^2-1)#
Substitute.
#=>int1/(tan(theta))sec(theta)tan(theta)d theta# Simplify
#=>intsec(theta)d theta#
This is one of the "basic" integrals you should memorize.
#=>lnabs(sec(theta)+tan(theta))# substitute
#=>lnabs(sec(arcsec(x))+tan(arcsec(x)))#
#=>lnabs(x+tan(arcsec(x)))#
Therefore:
#int_-3^-2 1/(sqrt(x^2-1))dx=[lnabs(x+tan(arcsec(x)))]_-3^-2#
#=>lnabs(-3+tan(arcsec(-3)))-lnabs(-2+tan(arcsec(-2)))#
#=>1.76274717404-1.31695789692#
#=>0.44578927712#
That is the answer!

