This is a little tough; it's just long and requires a lot of steps. Don't be intimidated. You can do it and I can help show you how.
#intsqrt(x^2-1)dx#
First do a trigonometric substitution
Let #x=sectheta#
#dx=secthetatanthetad(theta)#
#sqrt(x^2-1)=sqrt((sectheta)^2-1)=sqrt(sec^2theta-1)=sqrt(tan^2theta)=tantheta#
Make the substitution:
#intsqrt(x^2-1)dx=int(tantheta)secthetatanthetad(theta)#
You may now proceed by using trigonometric identities.
#inttan^2thetasecthetad(theta)#
#=int(sec^2theta-1)secthetad(theta)#
#=intsec^3theta-secthetad(theta)#
#=intsec^3thetad(theta)-intsecthetad(theta)#
#=intsec^3thetad(theta-lnabs(sectheta+tantheta)#
The first integral can be solved using integration by parts:
#intsec^3thetad(theta)=intsec^2thetasecthetad(theta)#
#u=sectheta#
#du=secthetatanthetad(theta)#
#dv=sec^2thetad(theta)#
#v=tantheta#
#secthetatantheta-inttanthetasecthetatanthetad(theta)#
#=secthetatantheta-inttan^2thetasecthetad(theta)#
Notice that we have our original integral back. It would seem that we are not getting anywhere. Try this trick. Set the original integral equal to what we have so far.
#inttan^2thetasecthetad(theta)=secthetatantheta-inttan^2thetasecthetad(theta)-lnabs(sectheta+tantheta)#
Get like terms together:
#2inttan^2thetasecthetad(theta)=secthetatantheta-lnabs(sectheta+tantheta)#
Divide both sides by two to solve the integral. Don't forget to add the constant of integration.
#inttan^2thetasecthetad(theta)=1/2(secthetatantheta-lnabs(sectheta+tantheta))#
But wait, we're not done yet!
To get back to the original variable, #x#, you must make a right triangle.
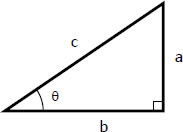
Recall that #sectheta=c/b# and that our substitution defined #sectheta=x/1#
That means that #c=x# and #b=1#.
Now, using the pythagorean theorem, we find #a#
#a^2+b^2=c^2#
#a^2+1^2=x^2#
#a^2=x^2-1#
#a=sqrt(x^2-1)# (our original root)
Therefore, #tantheta=sqrt(x^2-1)/1=sqrt(x^2-1)#
Taking these values and substituting them into our answer, we get:
#intsqrt(x^2-1)dx=1/2(xsqrt(x^2-1)-lnabs(x+sqrt(x^2-1)))+C#

