How do you integrate #(sinx)(cosx)(cos2x)dx#?
2 Answers
Mar 15, 2015
First use a double-angle formula to replace
Mar 15, 2015
You can try this:
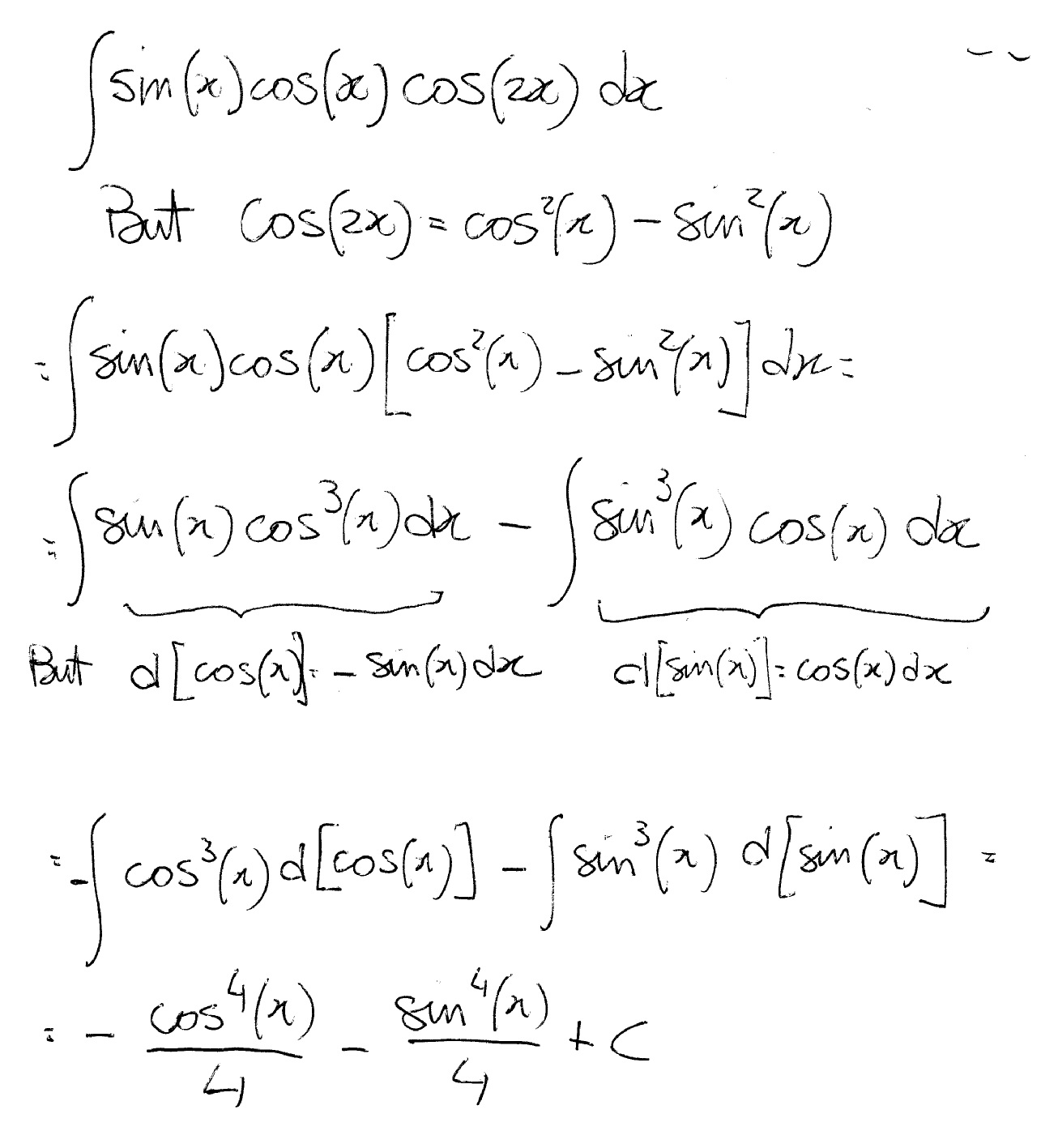
where at the end you treat


