This integral does not seem solvable by other techniques, e.g. integration by part, just integration by trigonometric substitution.
On integration by trigonometric substitution, you either apply trigonometry or trigonometric functions, such as the one herein. Unfortunately there is no general recipes, just training. The trick is reducing the integral to a manageable state; the only way is trying.
Replace: #x=5/costheta#; how do I know that? unfortunately, there is no way to explain it, it is a "guess and try" game.
Now you should transform the infinitesimal variable #dx#, why? remember that in math everything should be coherent, such as, if you change the limits of integration, you must apply a proper transformation.
#dx=5/cos^2theta*sintheta d theta#
In order to arrive to this, it was applied the substitution rule:
#u=costheta#, #x=5/u#, remember the basic derivatives, #dx/(d theta)=-5/u^2(du)/(d theta)#, if you are not familiar, you must go back one step forward in your calculus life, and train. It is called the substitution method, quite needed. Remember that the derivative of #costheta# is #-sintheta#.
We should simplify, remember #x=5/costheta# :
#sqrt(x^2 - 25)/x= sqrt(25/cos^2theta - 25)/(5/costheta)#
Basic rules from mathematics:
#sqrt(25/cos^2theta - 25)costheta/5#
#sqrt(1/cos^2theta - 1)costheta#
#sqrt(1 - cos^2theta)=sintheta#; here just apply #cos^2theta + sin^2theta=1#
Finally,
#sqrt(x^2 - 25)/x= sintheta#
So, remember that #tantheta=sintheta/costheta#:
#intsqrt(x^2 - 25)/xdx=5intsin^2theta/cos^2thetad theta#
#intsqrt(x^2 - 25)/xdx=5inttan^2thetad theta#
By using a table of integrals:
#5inttan^2thetad theta=5*(tantheta -theta + C)#
Where, #C# is a constant.
remember #x=5/costheta#, #costheta=5/x#, #theta=arccos(5/x)#
Finally:
#intsqrt(x^2 - 25)/xdx=5*(tanarccos(5/x) -arccos(5/x) + C)#
See:
https://en.wikipedia.org/wiki/Lists_of_integrals
https://en.wikipedia.org/wiki/List_of_integrals_of_trigonometric_functions
Guessing the "magic"
Our problem falls into the third case of the scheme below, replace u by x and a by 5.
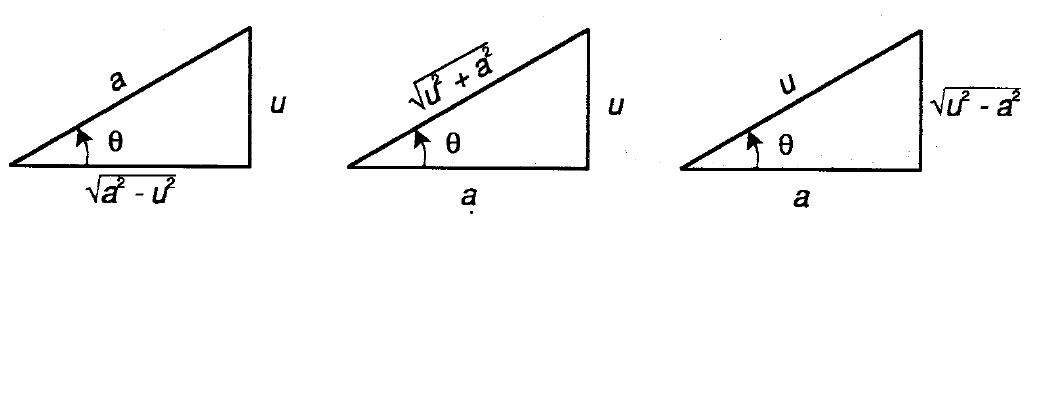
We get #sintheta=sqrt(x^2 - 25)/x#
Further:
#sintheta=sqrt(x^2 - 25)/x#
#sin^2theta=1 - 25/x^2#
#25/x^2=1 - sin^2theta#
#25/x^2=cos^2theta#
#25/cos^2theta=x^2 #
#x=5/costheta #
The rest you already know.
Hand calculations





