How do you know if #x+2y=4# and #2x+4y=5# is consistent or inconsistent?
1 Answer
Your system is inconsistent.
You can see this first by looking at it....at least for the
This means that the 2 lines, that represents graphically your equations, are PARALLEL!!! The independence of the free coefficients (
Then you can also try to substitute one equation into the other and you'll find a CONTRADICTION.
For example:
From the first:
You can also try to subtract one equation from the other (multiplied by a constant):
For example:
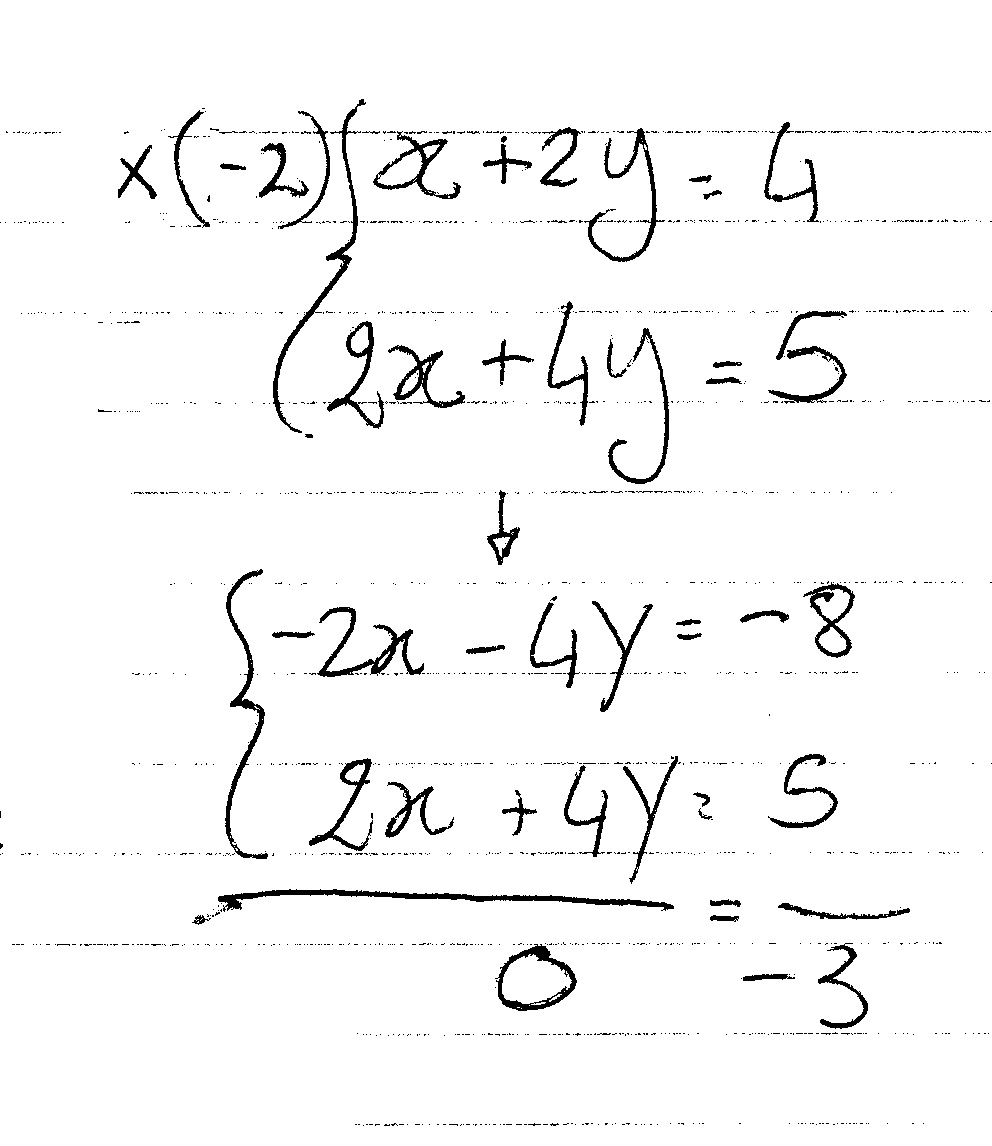
Which is again not true!

