How many solutions do the system of equations #2x-3y=4# and #4x-6y =-7# have?
1 Answer
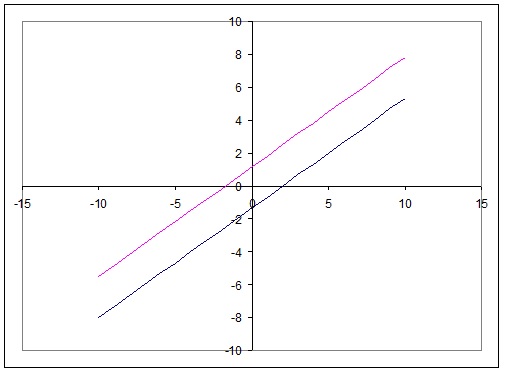
Each equation in your system represents a straight line...the only thing is that the two lines in your case are parallel!!!! So your system doesn't have solutions (basically the two lines never meet!!!).
You can see this because the second equation has the
Basically it means that your two lines have the same slope (inclination) and cross the
Rearranging you get:
You can see that the slope of your two lines (the coeficient of
Graphically you can see this even more easily plotting the two lines as: