The partial derivatives of #z=f(x,y)=x^2+9y^2-x*y# are #(partial z)/(partial x)=2x-y# and #(partial z)/(partial y)=18y-x#. Setting these equal to zero and solving for #x# and #y# give only one critical point, at the origin #(x,y)=(0,0)#, which is not in the domain #3 leq xy leq 5#.
Therefore, the maximum and minimum values of #f#, if any, must occur along the boundary of the domain, where either #xy=3# or #xy=5#. Using the function #g(x,y)=xy#, these conditions can be written as #g(x,y)=3# and #g(x,y)=5#.
The Method of Lagrange Multipliers can now be used. The gradient vector of #f# is #nabla f=<2x-y,18y-x># and the gradient vector of #g# is #nabla g= < y,x >#. Setting #nabla f=lambda nabla g#, along with the constraint equation, results in the system #2x-y=lambda y#, #18y-x=lambda x#, and, for the first boundary curve, #xy=3#, while for the second boundary curve, #xy=5#.
We then have #(2x-y)/y=lambda=(18y-x)/x# whenever #y !=0# (for the first equation) and #x !=0# (for the second equation). Cross-multiplication of this leads to #2x^2-xy=18y^2-xy#, or #x^2=9y^2#, or #x=pm 3y#. Since we are in the first quadrant, we use #x=3y# to get #3y*y=3 \Rightarrow y=1 \Rightarrow x=3# for the first boundary curve (#xy=3#) and #3y*y=5\rightarrow y=sqrt(5/3)\rightarrow x=sqrt(15)# for the second boundary curve.
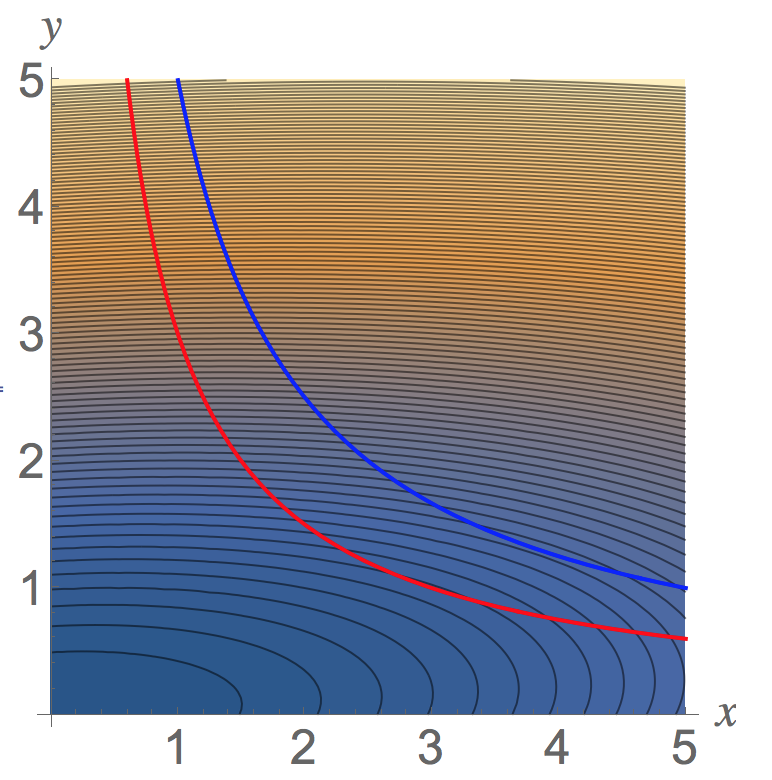
If you now look at the contour map of the level curves (shown further below...dark means smaller outputs and light means higher outputs), you'll see that a global minimum for #f# occurs on the lower (left) boundary curve at #(x,y)=(3,1)#, with a global minimum value of #f(3,1)=15#.
A local minimum value for #f# along the upper (right) boundary curve occurs at #(x,y)=(sqrt(15),sqrt(5/3))# with local minimum value #f(sqrt(15),sqrt(5/3))=25#. You can also see there are no global maximum values (the function output keeps going up and up without bound as you move up and up between the boundary curves without bound.