With the so called slack variables #s_1, s_2# we transform the maximization/minimization with inequality constraints problem, into a formulation amenable for the Lagrange Multipliers technique.
Now the lagrangian formulation reads:
minimize/maximize
#f(x,y) =x - x y^2#
subjected to
#g_1(x,y,s_1) = x^2 + y -s_1^2 -1=0#
#g_2(x,y,s_2) = x^2 + y +s_1^2 -3=0#
forming the lagrangian
# L(x,y,s_1,s_2,lambda_1,lambda_2) = f(x,y)+lambda_1g_1(x,y,s_1)+lambda_2 g_2(x,y,s_2)#
The local minima/maxima points are included into the lagrangian stationary points found by solving
#grad L(x,y,s_1,s_2,lambda_1,lambda_2) = vec 0#
or
#{
(1 + 2 (lambda_1 + lambda_2) x - y^2=0),
(lambda_1 + lambda_2 - 2 x y = 0),
(s_1^2 - x^2 - y=0),
(lambda_1 s_1 = 0),
(s_2^2 + x^2 + y - 1=0),
(lambda_2 s_2 = 0)
:}#
Solving for #x,y,s_1,s_2,lambda_1,lambda_2# we obtain
#(
(x = 0, y=1., lambda_1 = 0, s_1 = -1., lambda_2= 0, s_2 = 0),
(x = -1.09545, y= -0.2, lambda_1 = 0, s_1= -1., lambda_2 = 0.438178,
s_2 = 0),
(x = 1.09545, y= -0.2, lambda_1= 0, s_1= -1., lambda_2 = -0.438178,
s_2 = 0),
(x = -0.66874, y= -0.447214, lambda_1 = 0.59814, s_1 =0, lambda_2 = 0, s_2= -1.),
(x = 0.66874, y= -0.447214, lambda_1 = -0.59814, s_1 = 0, lambda_2 = 0, s_2 = -1.)
)#
Those five points must be qualified. The first second and thirt activate constraint #g_2(x,y,0)# and the two other activate constraint #g_1(x,y,0)# Their qualification will be done with
#f@g_1 (x) =x - x^5# and
#f@g_2(x) =-x^3 (x^2-2)#
giving
#d^2/(dx^2)f@g_1 ( -0.66874) =5.9814# local minimum
#d^2/(dx^2)f@g_1 (0.66874) = 5.90567# local maximum
#d^2/(dx^2)f@g_2 (0) = 0# not decidable
#d^2/(dx^2)f@g_2 (-1.09545) = 13.1453# local minimum
#d^2/(dx^2)f@g_2 ( 1.09545) =-13.1453# local maximum
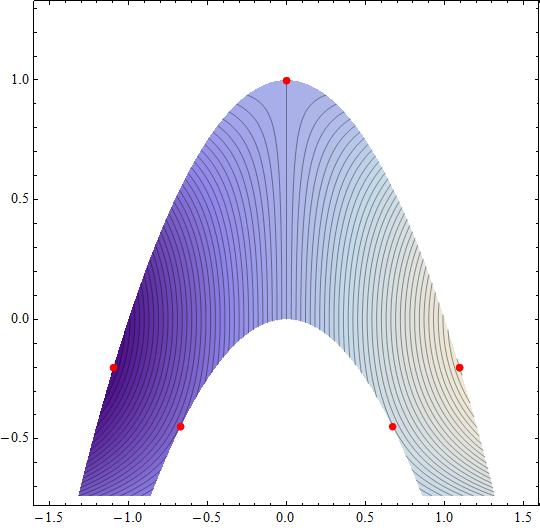
Attached a figure with the #f(x,y)# contour map inside the feasible region, with the local maxima/minima points.