Determine the formula for the Volume of the cylinder contained within a 1 m radius sphere relative to the radius of the cylinder.
Differentiate to establish critical points.
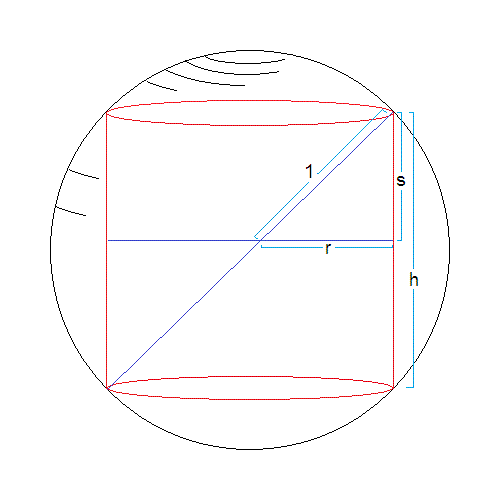
Volume of cylinder (#V#) #= pi r^2h = 2 pi r^2 s#
where #s# is the semi-height.
#r^2 + s^2 = 1 rarr s = sqrt(1-r^2)#
so
#V(r) = 2pi r^2 * (1-r)^(1/2)#
#(d V(r))/(dr) = 2pi ( (d r^2)/(dr)*(1-r^2)^(1/2) + r^2 (d (1 - r^2)^(1/2) )/(dr) )#
Since
#(d r^2)/(dr) = 2r#
and
#(d (1-r^2)^(1/2))/(dr) = (d (1-r^2)^(1/2))/(d(1-r^2)) * (d (1-r^2))/(dr)#
#= (- r) (1-r^2)^(- 1/2)#
#(d V(r))/(dr) = 2pi (2r (1-r^2)^(1/2) + r^2( (-r)/(sqrt(1-r^2))))#
#= 2 pi ( 2rsqrt(1-r^2) - (r^3)/(sqrt(1-r^2)))#
Set #(d V(r))/(dr) = 0# for critical points
#2 pi ( 2rsqrt(1-r^2) - (r^3)/(sqrt(1-r^2)))= 0#
If #r != 0# we can divide by #2 pi r#
#2 sqrt(1-r^2) - (r^2)/(sqrt(1-r^2)) = 0#
If #r != 1# we can multiply by #sqrt(1-r^2)#
#2 (1-r^2) - r^2 = 0#
#2 - 3r^2 = 0#
#r = sqrt(2/3)#
Substituting we can find
#s = (1 - 2/3)^(1/2) = sqrt(1/3)#
and
#h = 2 sqrt(1/3)#
Note the extraneous possibilities #r=0# and #r=1# give the minimum cylinder size (which should be obvious from observation).

