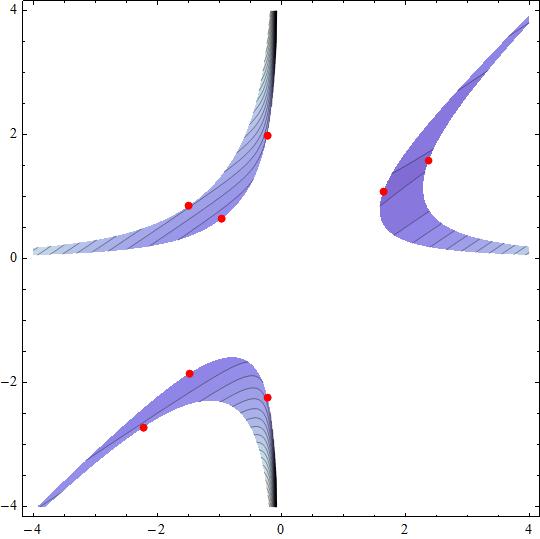
We will searching for stationary points, qualifying then as local maxima/minima.
First we will transform the maxima/minima with inequality restrictions into an equivalent maxima/minima problem but now with equality restrictions.
To do that we will introduce the so called slack variables #s_1# and #s_2# such that the problem will read.
Maximize/minimize #f(x,y) =(2 x - 3 y)^2 - 1/x^2#
constrained to
#{
(g_1(x,y,s_1)=x^2 y - x y^2 - s_1^2 - 1=0),
(g_2(x,y,s_2)=x^2 y - x y^2 + s_2^2 - 3=0)
:}#
The lagrangian is given by
#L(x,y,s_1,s_2,lambda_1,lambda_2) = f(x,y)+lambda_1 g_1(x,y,s_1)+lambda_2g_2(x,y,s_2)#
The condition for stationary points is
#grad L(x,y,s_1,s_2,lambda_1,lambda_2)=vec 0#
so we get the conditions
#{
(2/x^3 + 4 (2 x - 3 y) + lambda_1 (2 x y - y^2) +
lambda_2 (2 x y - y^2) = 0),
(-6 (2 x - 3 y) + lambda_1 (x^2 - 2 x y) +
lambda_2 (x^2 - 2 x y) = 0),
( -1 - s_1^2 + x^2 y -
x y^2 = 0),
(-2 lambda_1 s_1 = 0),
(-3 + s_2^2 + x^2 y - x y^2 = 0),
(2 lambda_2 s_2 = 0)
:}#
Solving for #{x,y,s_1,s_2,lambda_1,lambda_2}# we have
#{
(x = -1.47669, y= -1.84394, lambda_1= -4.73797, s_1 = 0., lambda_2 = 0., s_2= -1.41421),
(x = -0.964714, y= 0.64425, lambda_1= -10.6606, s_1= 0., lambda_2= 0., s_2 = -1.41421), (x= -0.227896, y= 1.9839, lambda_1 = -40.2068, s_1 = 0., lambda_2 = 0., s_2= -1.41421), (x= -0.219711, y= -2.24609, lambda_1= -40.2608, s_1 = 0., lambda_2= 0., s_2 = -1.41421), (x = 1.64519, y = 1.08494, lambda_1 = -0.247151, s_1= 0., lambda_2= 0., s_2= -1.41421),
(x = -2.22844, y = -2.72286, lambda_1 = 0., s_1 = -1.41421, lambda_2 = -3.10624, s_2 =0.),
(x = -1.49657, y= 0.853125, lambda_1= 0., s_1 = -1.41421, lambda_2= -6.95042, s_2 = 0.), (x= -0.0742241, y = 6.32052, lambda_1 = 0., s_1= -1.41421, lambda_2= -121.49, s_2 = 0.), (x = -0.0739366, y = -6.40695, lambda_1 = 0., s_1 = -1.41421,lambda_2 = -121.491,s_2=0.),
(x = 2.37908, y= 1.58197, lambda_1 = 0., s_1= -1.41421, lambda_2 = -0.0392951, s_2 = 0.)
:}#
so we have 10 points which are potential local maxima/minima points. The first 5 points activate #g_1(x,y,0) = 0# and the last 5 activate restriction #g_2(x,y,s_2) = 0#
The first 5 points must be evaluated on
#f_{g_1}(x,y) = (2 + 18 x - 5 x^4 pm 3 x^(5/2) sqrt[x^3-4])/(2 x^2)#
and the last 5 on
#f_{g_2}(x,y)=(2 + 54 x - 5 x^4 pm 3 x^(5/2) sqrt[x^3-12])/(2 x^2)#
After qualifying we obtain
#p_{max} = {-0.0742241,6.32052,0.}# maximum point of local maxima.