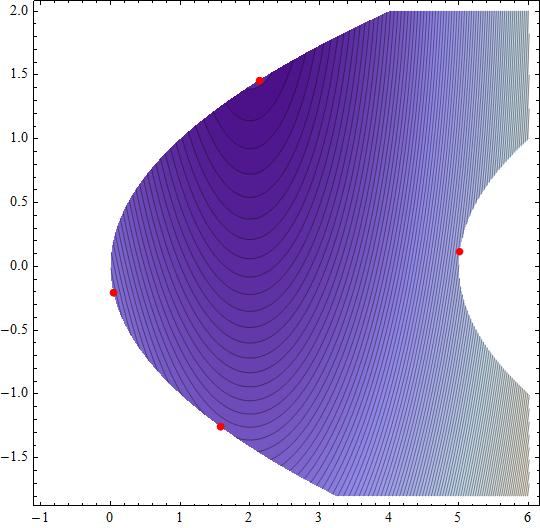
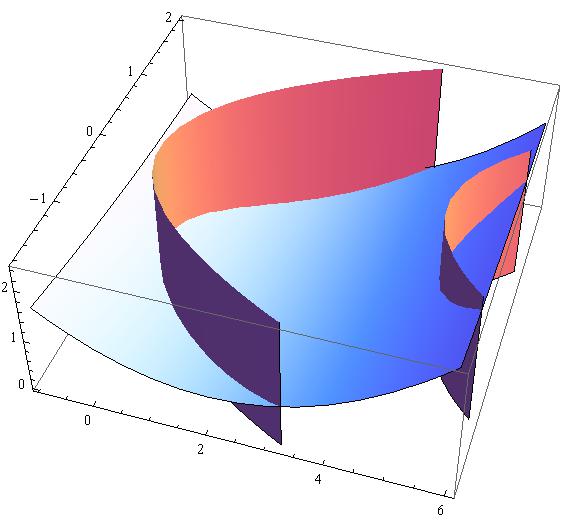
Using slack variables #s_1,s_2# to reduce the optimization problem to an equality restrictions one, the formulation can be stated as
min/max
#f(x,y) = (x - 2)^2/9 + (y - 3)^2/36#
subjected to
#g_1(x,y,s_1) = x - y^2 - s_1^2#
#g_2(x,y,s_1) = x - y^2 + s_2^2-5#
The lagrangian
#L(x,y,s_1,lambda_1,s_2,lambda_2) = f(x,y)+lambda_1g_1(x,y,s_1)+lambda_2g_2(x,y,s_2)#
is analytical so the determination of stationary points include the local maxima/minima points.
The stationary points are solutions of
#grad L(x,y,s_1,lambda_1,s_2,lambda_2) = vec 0#
for #x,y,s_1,lambda_1,s_2,lambda_2#
#{
(lambda_1 + lambda_2 + 2/9 (x-2)=0),
(1/18 (y-3) - 2 lambda_1 y - 2 lambda_2 y=0), (-s_1^2 + x - y^2=0),( -2 lambda_1 s_1=0),( -5 +
s_2^2 + x - y^2=0), (2 lambda_2 s_2=0)
:}#
giving
#(
(x = 2.13184, y = 1.46008,
lambda_1 = -0.0292967, s_1 = 0., lambda_2 = 0.,
s_2 = -2.23607),
(x = 0.0418471,
y = -0.204566,
lambda_1 = 0.435145, s_1 = 0., lambda_2 = 0.,
s_2 = -2.23607),
(x = 1.57632, y = -1.25551 ,
lambda_1 = 0.0941516, s_1 = 0., lambda_2 = 0., s_2 = -2.23607),
(x =5.01427, y = 0.119455, lambda_1 = 0., s_1 = -2.23607,
lambda_2 = -0.669838, s_2 = 0.)
)#
The first three points are located in the boundary defined by #g_1(x,y,0)=0# so must be qualified by #f_{g_1}#. The last is located in the boundary defined by #g_2(x,y,0)=0# and must be qualified by #f_{g_2}#
#f_{g_1}(x) = 1/36 (25 + 6 sqrt[x] - 15 x + 4 x^2)#
#d^2/(dx^2)f_{g_1}(x) = 2/9 - 1/(24 x^(3/2))#
#d^2/(dx^2)f_{g_1}(2.13184) = 0.208836# local minimum
#d^2/(dx^2)f_{g_1}( 0.0418471) =-4.64511# local maximum
#d^2/(dx^2)f_{g_1}( 1.57632) =0.201169# local minimum
and
#f_{g_2}(x) =1/36 ((sqrt[x-5])^2 + 4 (x-2)^2-3)#
#d^2/(dx^2)f_{g_2}(x) = 2/9 - 1/(24 (x-5)^(3/2))#
#d^2/(dx^2)f_{g_2}( 5.01427) =24.6667# local minimum
Attached the local extrema location with objetive function contours
and the surfaces involved.