Question

How do you minimize and maximize `f(x,y)=(x-y)/((x-2)^2(y-4))` constrained to `xy=3`?

Answer 1

Local maximum located at `(x = -4.89184, y =-0.613266)`

Explanation:

We will be looking for stationary points with posterior qualification.
This technique consists in finding points such that the normal vector to the objective function

`f(x,y)=(x - y)/((x - 2)^2 (y - 4))`

and the restriction function

`g(x,y)=x y - 3 = 0`

are aligned. Formally speaking, there exists `lambda` such that

`grad f(x,y)+lambda grad g(x,y) = vec 0`

proceeding this way we obtain the equation set

#{ (-((2 + x - 2 y)/((x-2)^3 (y-4))) +lambda y=0),( ( 4 - x)/((x-2)^2 (y-4)^2) + lambda x=0), (x y-3=0) :}#

Without much effort can be obtained the unique real solution

`(x = -4.89184, y =-0.613266, lambda= 0.00179817)`

Qualifying this point must be done considering the restriction so the easiest way to do that is substituting the restriction `g(x,y)` into the
objective function `f(x,y)` obtaining

`(f_g) (x) =(3 - x^2)/((x-2)^2 (4 x-3))`

then we can verify that `d/(dx)(f_g) (-4.89184) = 0`
and

`d^2/(dx^2)(f_g) (-4.89184)= -0.000965087`

qualifying this point as a local maximum.

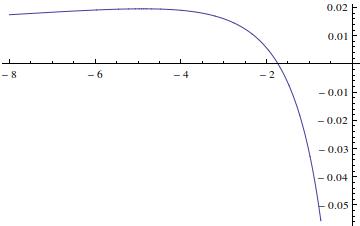
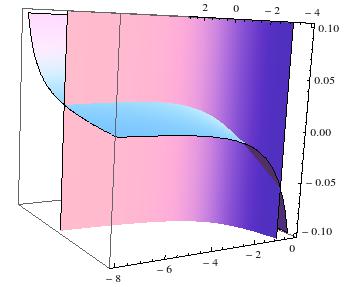
Attached are two figures. One representing the surface intersection of `f(x,y)` and `g(x,y)` and the other showing the function `(f_g) (x)`