How do you minimize and maximize #f(x,y)=(x-y)/((x-2)^2(y-4))# constrained to #xy=3#?
1 Answer
Local maximum located at
Explanation:
We will be looking for stationary points with posterior qualification.
This technique consists in finding points such that the normal vector to the objective function
and the restriction function
are aligned. Formally speaking, there exists
proceeding this way we obtain the equation set
Without much effort can be obtained the unique real solution
Qualifying this point must be done considering the restriction so the easiest way to do that is substituting the restriction
objective function
then we can verify that
and
qualifying this point as a local maximum.
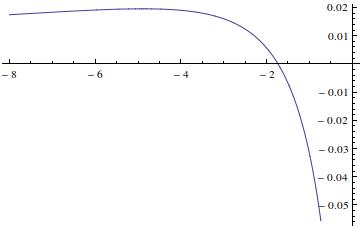
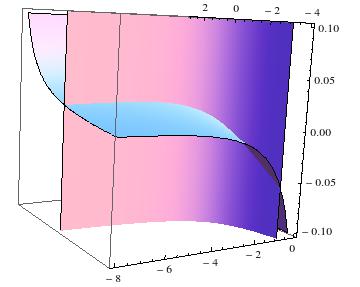
Attached are two figures. One representing the surface intersection of