How do you minimize and maximize #f(x,y)=(x-y)/(x^3-y^3)# constrained to #2 < xy <4 #?
Considering that #(x^3-y^3)/(x-y)=x^2+ xy+y^2# we have now the optimization problem
Find extrema of
#f(x,y) =1/(x^2+x y + y^2)#
subjected to
#g_1(x,y,s_1) = x y - 2 - s_1^2 =0#
#g_2(x,y,s_2) = x y - 4 + s_2^2=0#
#s_1,s_2# are known as slack variables. They are used to transform the inequality into equality relations.
The lagrangian is
#L(x,y,s_1,s_2,lambda_1,lambda_2)=f(x,y)+lambda_1g_1(x,y,s_1)+lambda_2g_2(x,y,s_2)# and it's stationary points are the points obeying
#grad L = vec 0# or
#{
(lambda_1 y + lambda_2 y - (2 x + y)/(x^2 + x y + y^2)^2 = 0),
(lambda_1 x + lambda_2 x - (x + 2 y)/(x^2 + x y + y^2)^2 = 0),
(-2 lambda_1 s_1 = 0),
(2 lambda_2 s_2 = 0),
(s_1^2 + x y - 2= 0),
(s_2^2 + x y - 4= 0):}#
Solving for #x,y,s_1,s_2,lambda_1,lambda_2# we obtain
#p_1,p_2,p_3,p_4#
#(
(x = -2., y = -2., s_1 = -1.41421, s_2 = 0, lambda_1 = 0, lambda_2 -> 0.0208333),
(x = 2., y= 2., s_1 = -1.41421, s_2 = 0, lambda_1= 0, lambda_2 = 0.0208333),
(x = -1.41421, y= -1.41421, s_1 = 0, s_2 = -1.41421, lambda_1 =0.0833333, lambda_2 = 0),
(x = 1.41421, y = 1.41421, s_1 = 0, s_2= -1.41421,
lambda_1= 0.0833333, lambda_2 = 0))#
The stationary points qualification is done according to the sign of
#(d^2(f@g_1)(s_1=0))/(dx^2)# and
#(d^2(f@g_2)(s_2=0))/(dx^2)#
Here
#(f@g_1)(x) = 1/(2 + 4/x^2 + x^2)#
#(f@g_2)(x) = 1/(4 + 16/x^2 + x^2)#
and
#(d^2(f@g_1)(s_1=0))/(dx^2) < 0# and
#(d^2(f@g_2)(s_2=0))/(dx^2) < 0# for all points so
#p_1,p_2,p_3,p_4# are all local maxima.
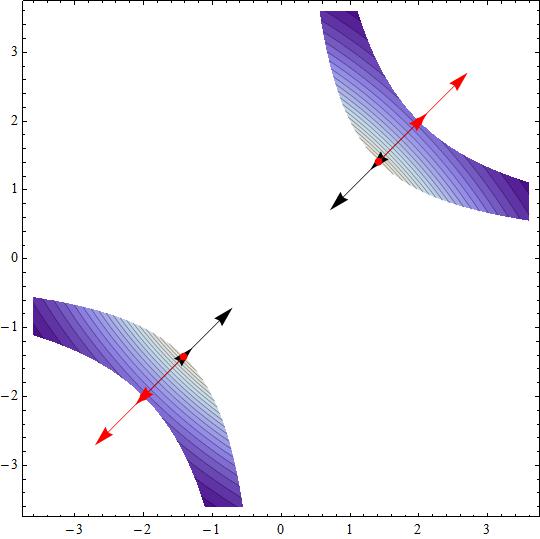
Attached a plot showing the feasible region and the points location.