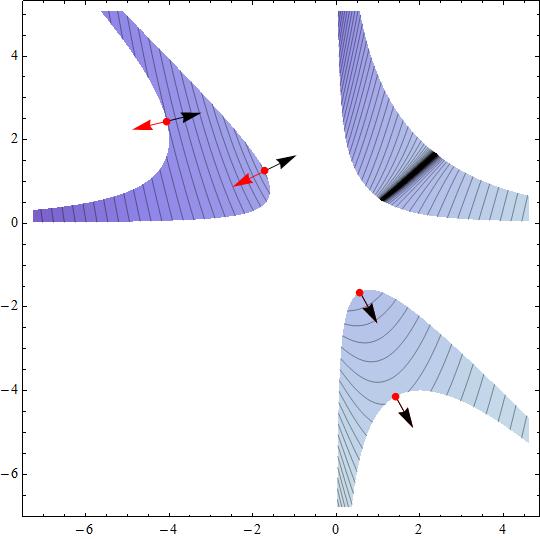
How do you minimize and maximize #f(x,y)=x-y/(x-y/(x-y))# constrained to #1<yx^2+xy^2<16#?
1 Answer
Feb 20, 2017
See below.
Explanation:
This problem can be successfully handled with the Lagrange Multipliers technique.
The local maxima/minima points are
Attached a plot showing the feasible region superimposed to the objective function level curves, with the local maxima/minima points.