How do you prove sin(90°-a) = cos(a)?
2 Answers
I prefer a geometric proof. See below.
Explanation:
If you're looking for a rigorous proof, I'm sorry - I'm not good at those. I'm sure another Socratic contributor like George C. could do something a little more solid than I can; I'm just going to give the lowdown on why this identity works.
Take a look at the diagram below:
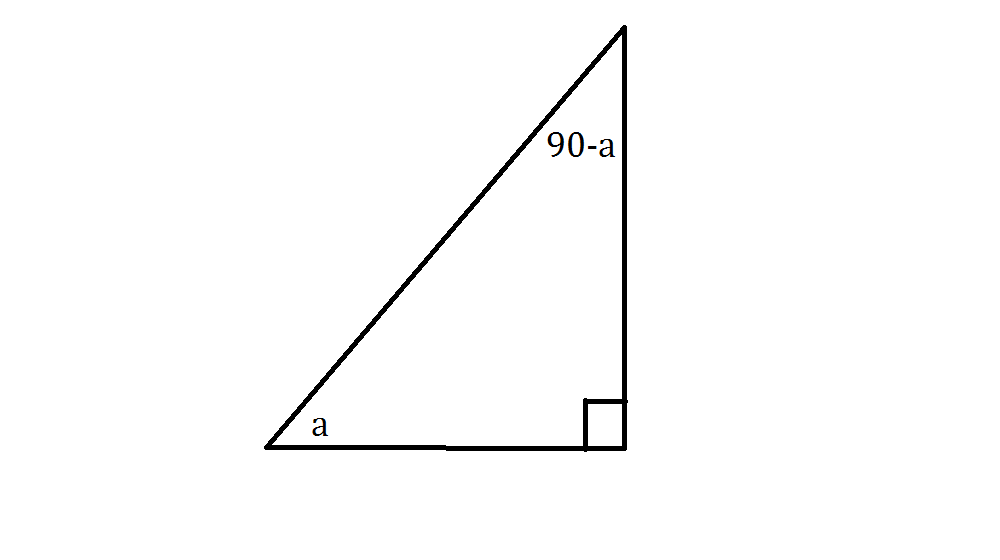
It's a generic right triangle, with a
We can see that the angles in our triangle do indeed add to
Now, let's add some variables for side length onto our triangle.
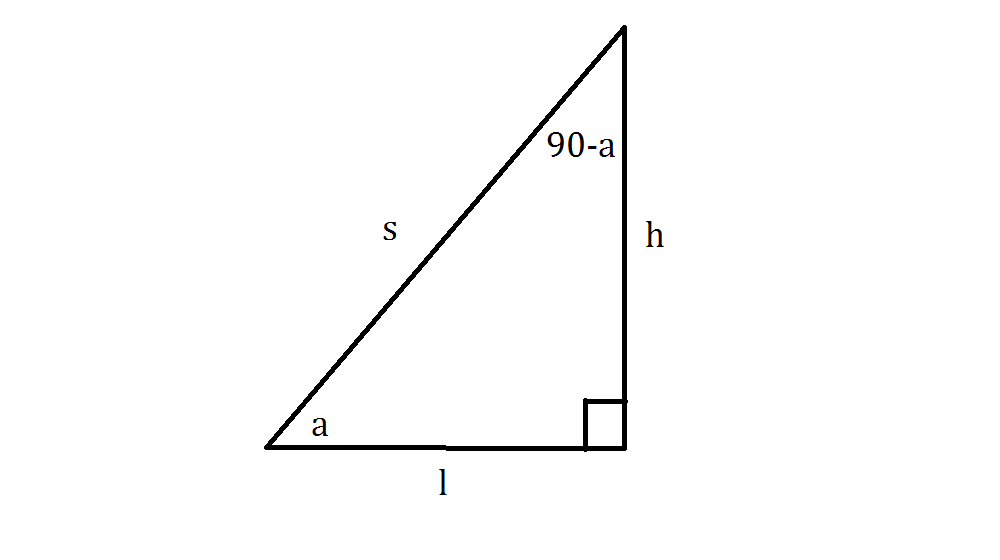
The variable
We can start on the juicy part now: the proof.
Note that
Note also that the cosine of the top angle,
So if
Then
And boom, proof complete.
sin (90 - a) = cos a
Explanation:
Another way is to apply the trig identity:
sin (a - b) = sin a.cos b - sin b.cos a
sin (90 - a) = sin 90.cos a - sin a cos 90.
Since sin 90 = 1, and cos 90 = 0, therefor,
sin (90 - a) = cos a

