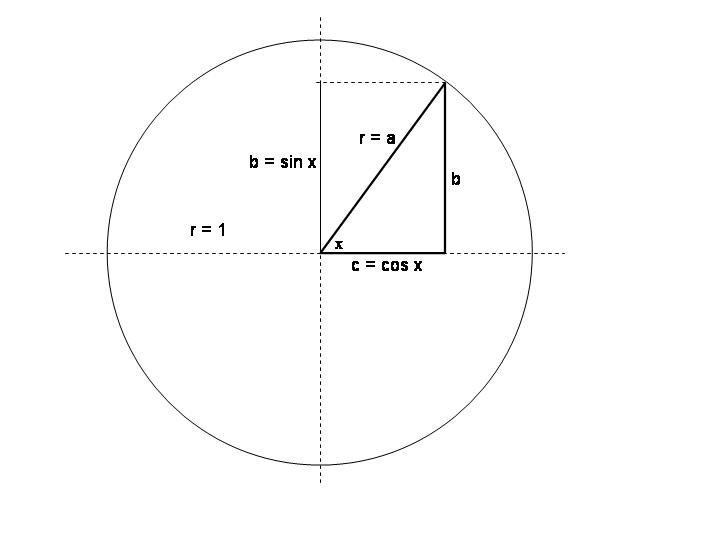
How do you prove the identity #(sin^2)x (cos^2)x=1 #?
1 Answer
Oct 19, 2015
Using the Pythagorean Theorem.
Explanation:
Sin and cos form the two legs (b) and (c) of a right triangle, and it's hypotenuse (a) is the radius of the trigonometric circle (r = a = 1).
According to Pythagoras: