How do you simplify (2x^3-32x)/(x^2+8x+16)?
2 Answers
Mar 28, 2018
See below
Explanation:
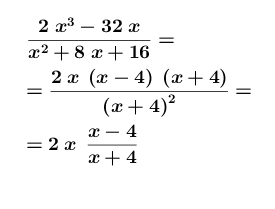
Mar 28, 2018
Explanation:
You cannot cancel despite it being so tempting to do so.
There are
Factorise first.


