How do you simplify #(sqrt12 - sqrt2)(sqrt12 + sqrt2)#?
2 Answers
Explanation:
To simplify
So
Explanation:
There are two ways to solve this, and I'm going to show the longer way first.
METHOD 1:
To solve this, we distribute and expand using the FOIL method:
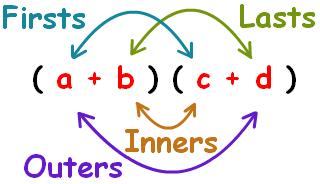
First, multiply the "firsts":
Then the "outers":
Then the "inners":
Finally the "lasts":
When we combine these expressions we get:
The
Which simplifies down to:
METHOD 2:
To solve this, we use:
This expression
As we can see, this is equivalent to
Simplify:
So the final answer is:
Hope this helps!


