How do you simplify #x^2/(x^2-4) = x/(x+2)-2/(2-x) #?
1 Answer
The given equation represents an impossible relation,
...unless (see below)
Explanation:
If we attempt to simplify the given equation (by multiplying both sides by
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As an alternative answer to the one given above, it is possible to claim a pair of solutions:
and if we look at the graphs for the left and right sides of the given equation this (sort of) makes sense:
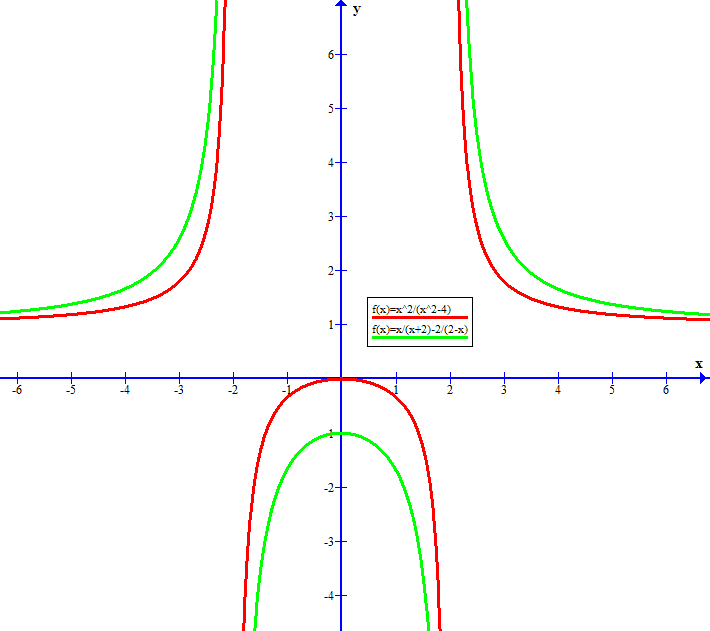
The limits at
