Clearing Denominators in Rational Equations
Key Questions
-
The least common multiple helps you to deal with expressions in which you must add or subtract fractions.
There are mnemonic rules to deal with this but I like to "see" the problem...
Imagine that you are out eating a pizza with some friends (3 for example). If your pizza comes divided in 4 slices it is ok...you can add 2 of them together and...presto...you have half pizza!!!
But if you start to cut one of the slices in half (someone is on a diet) and make another bigger (someone is not on a diet) the thing gets complicated...If you add two slices again you may find that you have a thin slice plus a big slice and...what part of the entire pizza you get? You do not know...!!!!
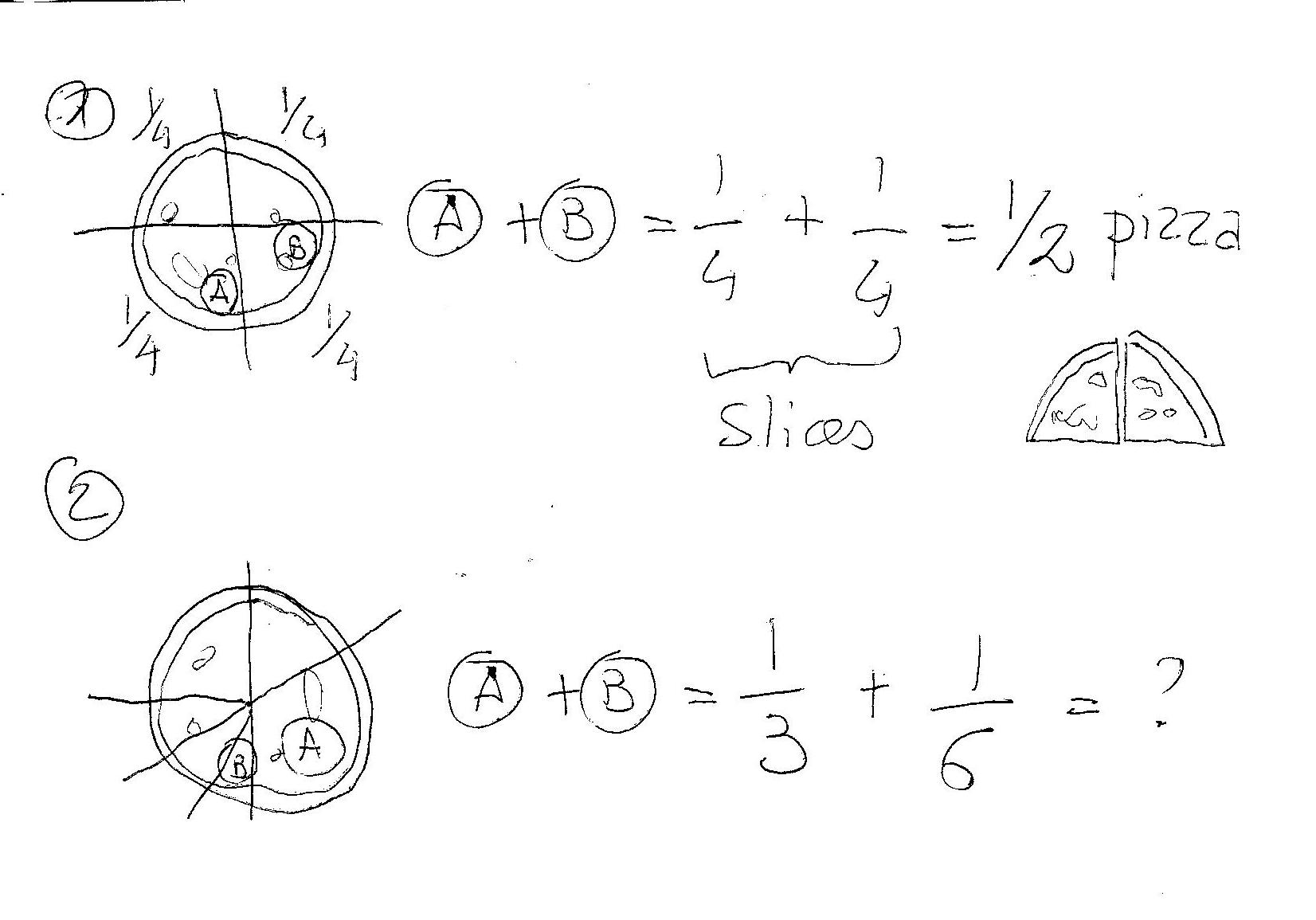
With fractions is the same...it is better to have equal slices to add them together!!!
In case 1 you can add together immediately the numerators because the denominators are equals (slices of same size!). And you get:
1/4+1/4=(1+1)/4=2/4=1/2 half pizza !!!!!In case 2 first you need to make the slices of the same "size". To do that you use a common size (the least common multiple) and you "resize" all your slices according to this size.
You have:
1/3+1/6 the least common multiple is a multiple in common between3 and 6 .
You have:
Multiples of3 :->3,6,9,12,....
Multiples of6 :->6,12,18,24,...
The least common multiple is6 . So now we resize all the slices to be "size"6 :
1/3 becomes of "size"6 if I multiply the denominator by2 but if I do that I have to multiply the nominator by2 as well (otherwise the fraction changes)!
1/3=(2*1)/(2*3)=2/6 Yes!!! Now it is "size"6 .
Now you have:
1/3+1/6=2/6+1/6 same denominator and you can add together the numerators:(2+1)/6=3/6=1/2 half pizza..again!!!Note that this work with subtraction as well!!!
-
I have created a video answer (with different examples) here: Clearing Fractions in Equations
Clearing denominators in rational equation is also known as clearing fraction in an equation. There are many times when a problem becomes easier to solve if you don’t have to worry about adding and subtracting fractions.
To clear the denominators you will need to multiply both sides of the equation by the smallest number both denominators divide evenly into.
Lets look at the problem:
x/2 + 5 = x/3 + 8 First we need to find the smallest number both 2 and 3 go into (or the LCD), which would be 6. Then we multiply both sides of the equation by that number.
6(x/2 + 5) = 6(x/3 +8) Using the distributive property, simplify the equation.
(6 * x/2) + (6 * 30) = (6 * x/3) + (6 * 8) 3x + 30 = 2x + 48 Now solving the equation as usual, we get
x = 18
Questions
Rational Equations and Functions
-
Inverse Variation Models
-
Graphs of Rational Functions
-
Division of Polynomials
-
Excluded Values for Rational Expressions
-
Multiplication of Rational Expressions
-
Division of Rational Expressions
-
Addition and Subtraction of Rational Expressions
-
Rational Equations Using Proportions
-
Clearing Denominators in Rational Equations
-
Surveys and Samples