How do you sketch the angle whose terminal side in standard position passes through $(2,-sqrt5)$ and how do you find sin and cos?

Question

2435 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-31T15:09:52

Letting the angle be $alpha$ , we get:
$sinalpha = -sqrt(5)/3$
$cosalpha = 2/3$

Draw a diagram:

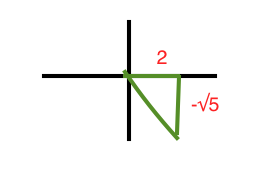
enter image source here

Since the angle between the two known sides is right, we can use pythagorean theorem to determine the length of the hypotenuse.

Let the hypotenuse be $x$ .

$(2)^2 + (-sqrt(5))^2 = x^2$

$4 + 5 = x^2$

$x^2 = 9$

$x = +-3$

A negative hypotenuse is impossible, so $x = 3$ , or the hypotenuse has a measure of $3$ units.

Note that the angle in standard position would be the angle of the triangle opposite the $-sqrt(5)$ .

Let the angle be $alpha$ .

$sinalpha = -sqrt(5)/3$

$cosalpha = 2/3$

Hopefully this helps!

How do you sketch the angle whose terminal side in standard position passes through (2,-sqrt5)(2,-sqrt5) and how do you find sin and cos?