How do you sketch the angle whose terminal side in standard position passes through (-3,1) and how do you find sin and cos?
1 Answer
Please see below.
Explanation:
To sketch the angle in standard position,
One side of the angle is the positive
The terminal side has one end at the origin (the point
Now draw a line from the origin through the point
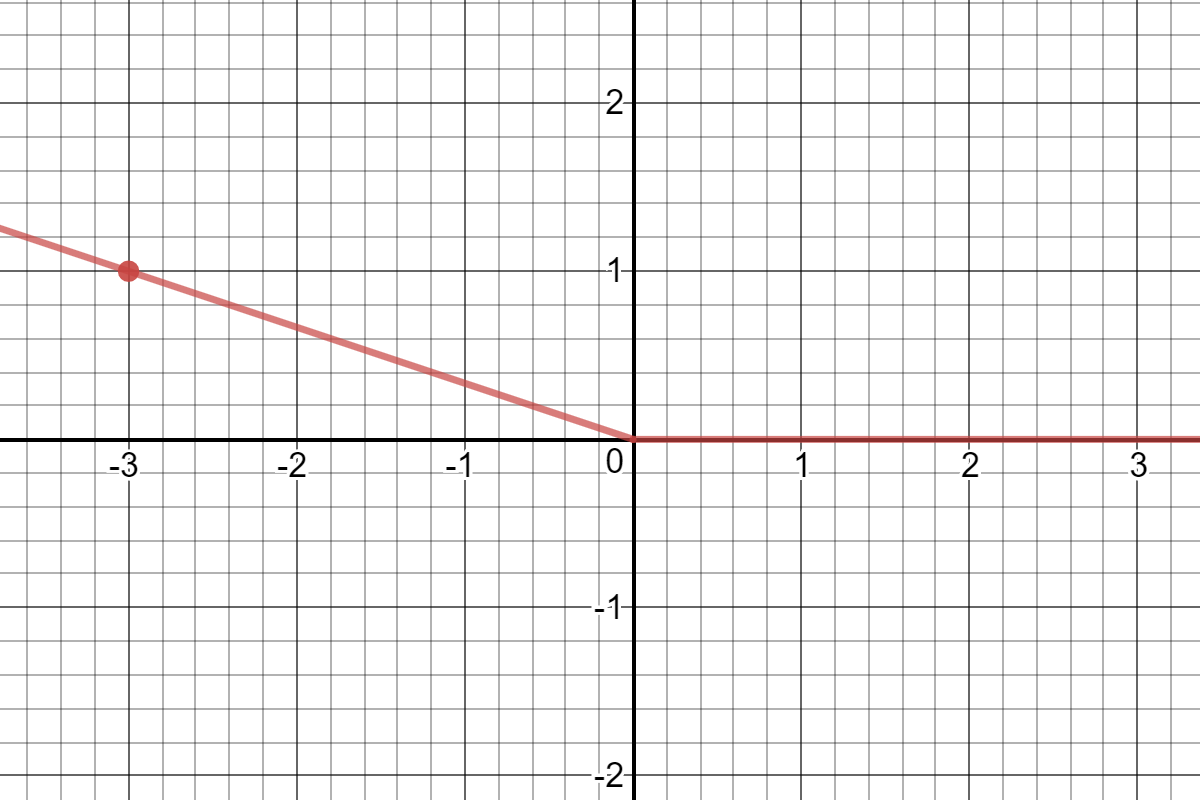
If we knew how the angle was made (which direction and how many times around the circle), we would show that also.
Give the angle a name. I will use
Memorize this
If the point
The angle has sine
For this question
We have
So the sine of
Many trigonometry teachers will insist that you write your answer with a rational number in the denominator. If this is something you have to do, multiply the answer by
So we should answer
The cosine of
Our answer is

