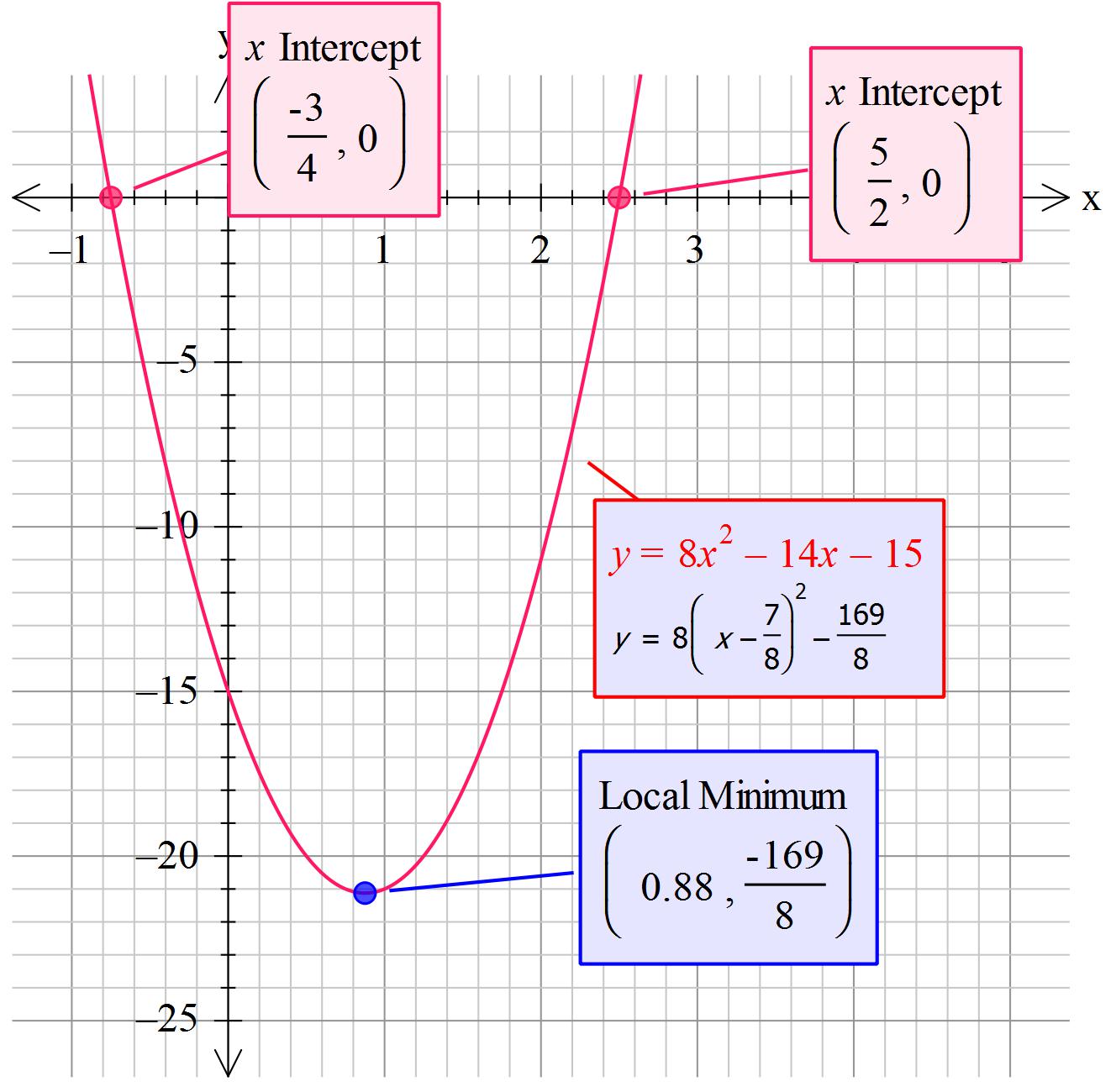
How do you solve #15=8x^2-14x#?

Question

1830 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-22T21:01:24

#color(blue)(color(green)( x = 7/8+-13/8) = 5/2 or 3/4)#

I am opting to use vertex form equation

Write as:#" "y=8x^2-14x-15#

Compare to standard form:#" "y=ax^2+bx+c#

Where#" "a=8"; "b=-14"; "c=-15#

Vertex form is:#" "y=a(x+b/(2a))^2 +c - a(b/(2a))^2#

#=>y=8(x-14/(2xx8))^2 -15-((-14)^2)/(4xx8)#

#=>y=8(x-7/8)^2 -169/8#

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Vertex "->(x,y)=(+7/8,-169/8)#

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Set #y=0# giving:

#169/64=(x-7/8)^2#

Taking the square root of both sides

#+-13/8 = x-7/8#

#color(blue)(=> x = 7/8+-13/8 = 5/2 or 3/4)#

Tony B